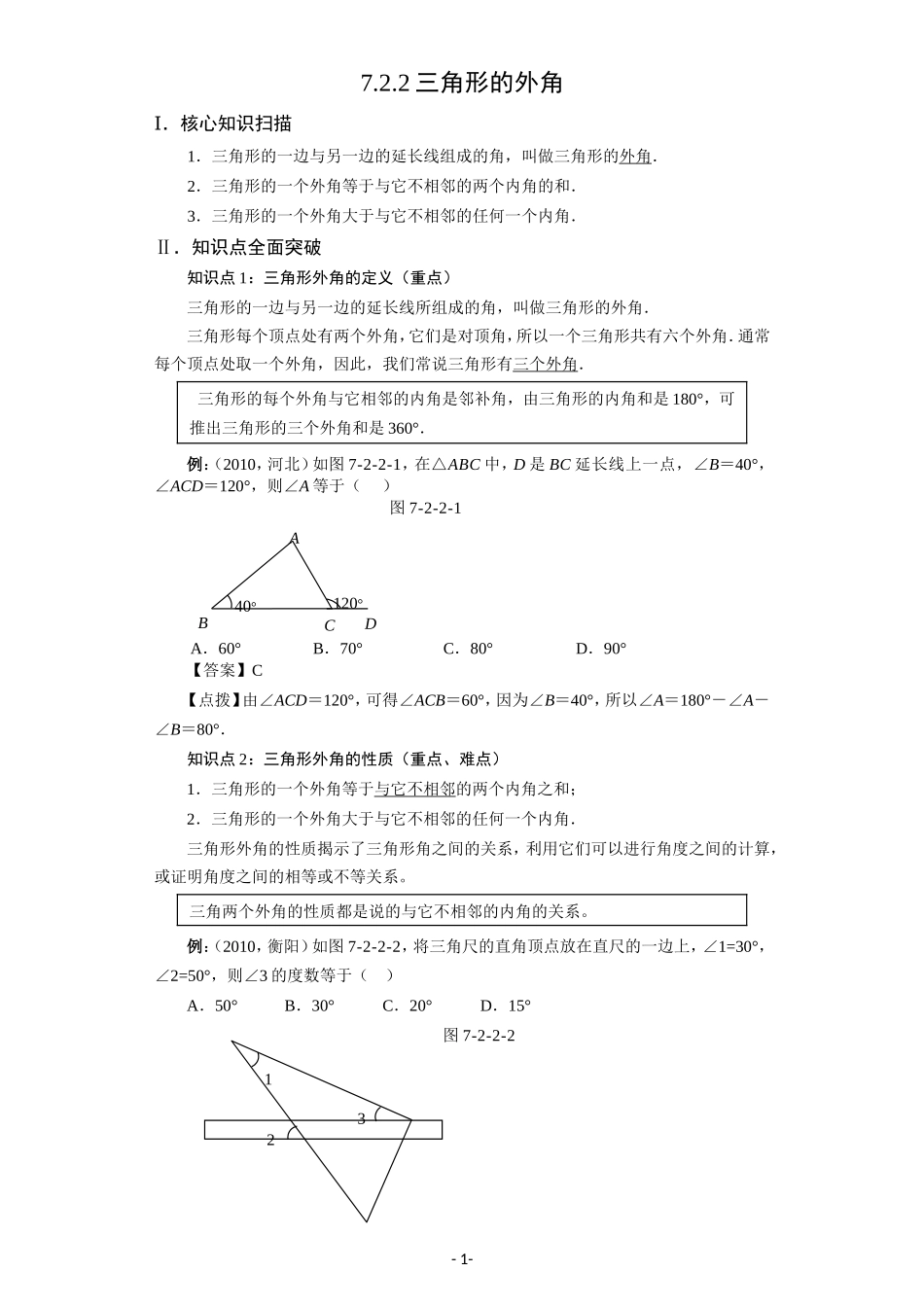
7.2.2三角形的外角Ⅰ.核心知识扫描1.三角形的一边与另一边的延长线组成的角,叫做三角形的外角.2.三角形的一个外角等于与它不相邻的两个内角的和.3.三角形的一个外角大于与它不相邻的任何一个内角.Ⅱ.知识点全面突破知识点1:三角形外角的定义(重点)三角形的一边与另一边的延长线所组成的角,叫做三角形的外角.三角形每个顶点处有两个外角,它们是对顶角,所以一个三角形共有六个外角.通常每个顶点处取一个外角,因此,我们常说三角形有三个外角.三角形的每个外角与它相邻的内角是邻补角,由三角形的内角和是180°,可推出三角形的三个外角和是360°.例:(2010,河北)如图7-2-2-1,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于()图7-2-2-1A.60°B.70°C.80°D.90°【答案】C【点拨】由∠ACD=120°,可得∠ACB=60°,因为∠B=40°,所以∠A=180°-∠A-∠B=80°.知识点2:三角形外角的性质(重点、难点)1.三角形的一个外角等于与它不相邻的两个内角之和;2.三角形的一个外角大于与它不相邻的任何一个内角.三角形外角的性质揭示了三角形角之间的关系,利用它们可以进行角度之间的计算,或证明角度之间的相等或不等关系。三角两个外角的性质都是说的与它不相邻的内角的关系。例:(2010,衡阳)如图7-2-2-2,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于()A.50°B.30°C.20°D.15°图7-2-2-2-1-ABCD40°120°123【答案】C【点拨】∠2的同位角正好是直尺上面的三角形的外角,因此∠2=∠1+∠3,故∠3=50°-30°=20°Ⅲ.提升点全面突破提升点1:利用外角进行角度的计算例1:如图7-2-2-3,∠C=48°,∠E=25°,∠BDF=140°,求∠A与∠EFD的度数。图7-2-2-3【解】 ∠BDF=∠C+∠CBD,∠C=48°,∠BDF=140°,∴∠CBD=92°, ∠CBD=∠A+∠E,∠E=25°,∴∠A=67°,∠EFD=∠A+∠C=115°【点拨】本题也可用三角形内角和定理来做,但用由于∠BDF是△BCD和△DEF的外角,因此本题利用外角的性质进行计算更加直接.例2:如图7-2-2-4,△ABC的三条角平分线交于点O,过O作OE⊥BC于E,求证:∠BOD=∠COECBAHGDEO图7-2-2-4【证明】 AD、BG、CH是△ABC的三条角平分线,∴∠ABG=∠ABC,∠BAD=∠BAC,∠BCH=∠ACB ∠ABC+∠BAC+∠ACB=180°,∴∠ABG+∠BAD+∠BCH=90°∴∠ABG+∠BAD=90°-∠BCH OE⊥BC,∴∠BCH+∠COE=90°∴∠COE=...