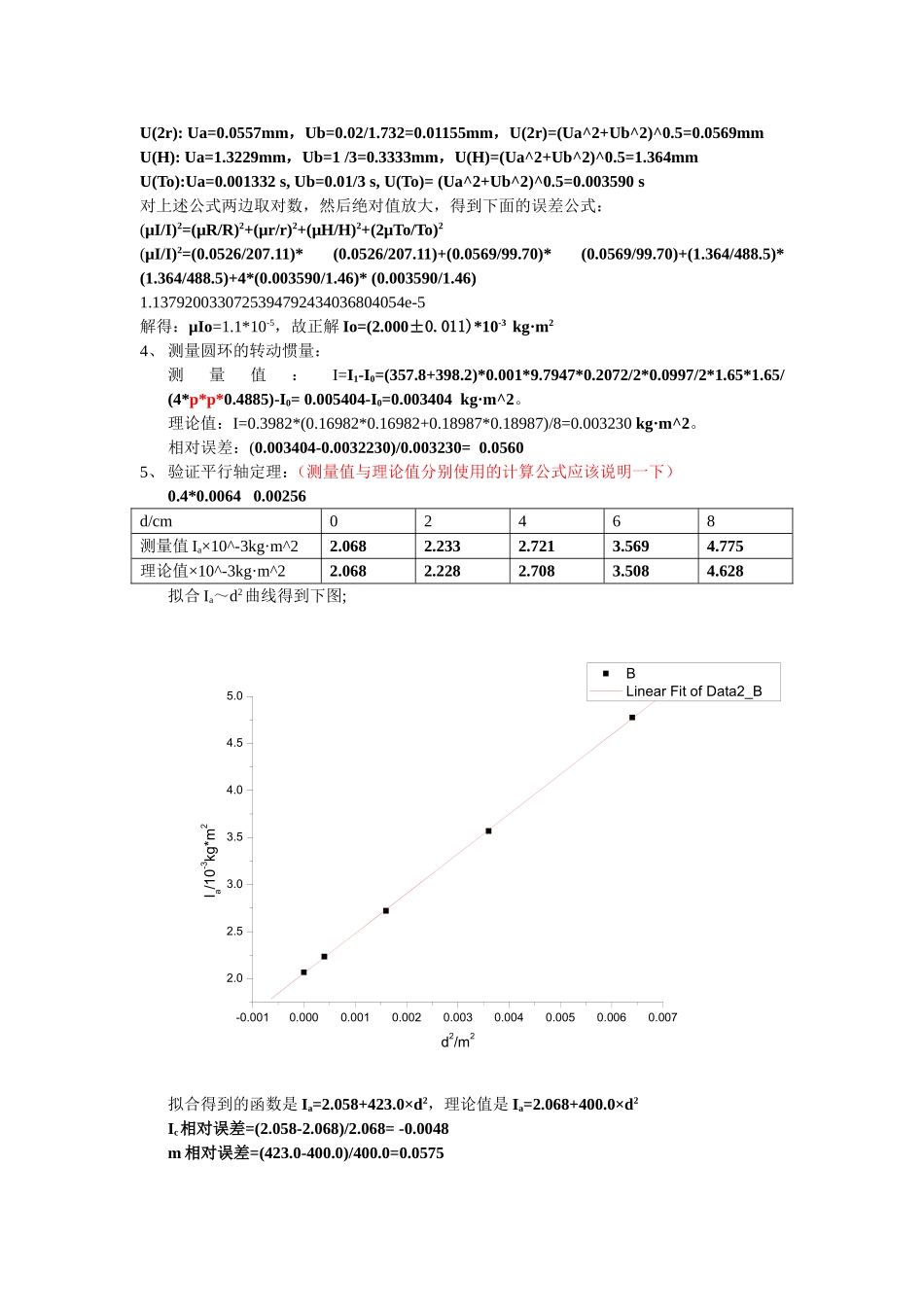
用三线摆测刚体的转动惯量(90)任志斌PB06210123实验目的1、掌握用三线摆测定物体转动惯量的方法;2、验证转动惯量的平行轴定理。实验原理1、三线摆转动原理:空载扭动时,将上圆盘绕竖直的中心轴线转动一个小角度,借助悬线的张力使得悬挂的大圆盘绕中心轴做扭摆运动。显然,扭转的周期与下圆盘的转动惯量有关。2、下圆盘的转动惯量:当转动角度很小时,可以得到下面的计算式子,其中m0、R、r、H和T0都可以测量,可以得到下圆盘的转动惯量Io。3、测量圆环的转动惯量:如果要测定一个质量为m的物体的转动惯量,可以将待测物体放在下圆盘的上面,并注意,必须让待测物体的质心恰好在仪器的转动轴线上,测定整个系统的转动周期T1,则系统的转动惯量I1可以由下式计算:式中H1为放了待测物体以后的上下圆盘间距,一般可以认为H1~H,待测物体的转动惯量I为:4、验证平行轴定理;用三线摆可以验证转动惯量的平行轴定理,物体的转动惯量取决于物体的形状的质量分布,以及相对于转轴的位置。因此,物体的转动惯量随转轴不同而改变,转轴可以通过物体内部,也可以在物体内部,根据平行轴定理,物体对于任意轴的转动惯量Ia,等于通过此物体以质心为轴的转动惯量Ic加上物体质量m与两轴距离d平方的乘积:通过改变待测物体质心与三线摆中心转轴的距离,测量Ia与d平方的关系便可以验证转动惯量的平行轴定理。实验内容调节上下盘面,使其处于水平,测定仪器常数R,r,H,m(各三次)1、测量下圆盘转动惯量Io,并计算不确定度(稳定后测50次,重复三次,取平均值,算出平均值To)(g取9.7947m/s*s)2、测量圆环的转动惯量,圆环I=1/8*m*(D1*D1+D2*D2)圆盘I=1/8m*D*D。3、验证平行轴定理,做出Ia~d^2,曲线,用回归法处理数据,将理论值与实验值做比较(d取0,2,4,6,8cm)。数据处理1、下圆盘质量mo=357.8g,圆环质量m1=398.20g,两线间距离a=173.36mm,金属圆柱质量m2=200.0g/个,g=9.7947m/s*s此处H的测量是用直尺立在桌子上测出上下圆盘的高度,桌面用水准仪检测过是水平的。还可以测出线的长度用几何方法算出H。单位cm第一次第二次第三次平均值标准差高度H60.40-11.4060.15-11.3560.25-11.5048.850.13229上圆盘直径2r9.9829.9609.9689.9700.01114下圆盘直径2R20.70020.71420.72020.7110.01026园环内直径D116.98416.98216.98016.9820.002园环外直径D218.98818.98418.99018.9870.003062、50次转动的时间记录:单位s第一次第二次第三次平均值周期TT的标准差盘1...