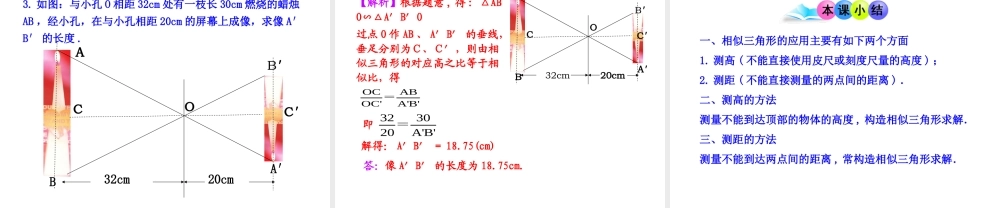
27.2.2相似三角形应用举例第1课时1.能应用相似三角形的有关知识解决一些实际问题;2.了解数学建模的思想,培养分析问题、解决问题的能力.相似三角形的判定(1)通过平行线.(2)三边对应成比例.(3)两边对应成比例且夹角相等.(4)两角相等.根据下列条件能否判定△ABC与△A′B′C′相似?为什么?(1)∠A=120°,AB=7,AC=14∠A′=120°,A′B′=3,A′C′=6(2)AB=4,BC=6,AC=8A′B′=12,B′C′=18,A′C′=21(3)∠A=70°,∠B=48°,∠A′=70°,∠C′=62°【例1】据史料记载,古希腊数学家、天文学家泰勒曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,如果木杆EF长2m,它的影子FD长为3m测得OA为201m,求金字塔的高度BO.如何测量OA的长?OAEF2012BO134.FD3因此金字塔的高为134m.解析:太阳光是平行光线,因此∠BAO=∠EDF,又∠AOB=∠DFE=90°,∴△ABO∽△DEFBO:EF=OA:FDPQRSTba【例2】如图为了估算河的宽度,我们可以在河对岸定一个目标点P,在近岸取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q垂直PS的直线b的交点R,如果测得QS=45m,ST=90m,QR=60m.求河的宽度PQ.解析: ∠PQR=∠PST=90°,∠P=∠P,∴△PQR∽△PST.PQ:PS=QR:ST,即PQ:(PQ+QS)=QR:ST,PQ:(PQ+45)=60:90,PQ×90=(PQ+45)×60,解得PQ=90.因此河宽大约为90m.如图,测得BD=120m,DC=60m,EC=50m,求河宽AB.解析: ∠B=∠C=90°,∠ADB=∠EDC,∴△ABD∽△ECD,AB:EC=BD:DC,AB=50×120÷60=100(m)ABDCE利用相似三角形测量瓶子的内径学具准备:等长的两根小木棒,橡皮筋,玻璃瓶,刻度尺过程:两人合作先把两根小木棒用橡皮筋捆好,然后将等长的两根小木棒的一端放进瓶子里,使两根小木棒抵住瓶底并紧靠瓶子的边缘,再用刻度尺测出小木棒另两端的距离.构造相似并计算瓶子内径.ODCBA【解析】设点O将两根小木棒都分成了1/n,如果我们测出线段AB的长度为m,根据两边对应成比例且夹角相等的两个三角形相似,我们就可以求出内径CD的长度了,即CD=mn.【规律方法】相似三角形的性质是我们常常用来证明线段等积式的重要方法,也是我们用来求线段的长度与角度相等的重要方法.如图,已知△ACB的边AB、AC上的点D、E,且∠ADE=∠C,求证:AD·AB=AE·AC.EDCBA【解析】 ∠ADE=∠C,∠A=∠A∴△ADE∽△ACB(如果一个三角形的两角与...