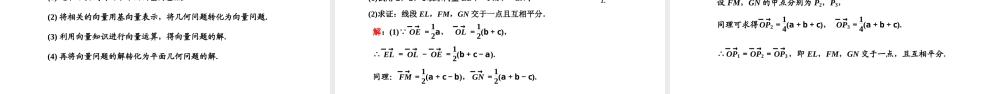6.3平面向量基本定理及坐标表示6.3.1平面向量基本定理明确目标发展素养1.了解向量的一个基底的含义,理解并掌握平面向量基本定理.2.在平面内,当一个基底选定后会用这个基底来表示其他向量.3.能灵活应用平面向量基本定理解决有关平面向量的综合问题.1.通过理解平面向量基本定理的概念,提升数学抽象、直观想象素养.2.通过运用平面向量基本定理解决问题,达成逻辑推理、数学运算素养.知识点平面向量基本定理(一)教材梳理填空平面向量基本定理:(1)定理:如果e1,e2是同一平面内的两个_______向量,那么对于这一平面内的_____向量a,_____________实数λ1,λ2,使a=____________.(2)基底:若e1,e2___________,我们把{e1,e2}叫做表示这一平面内______向量的一个基底.不共线所有不共线λ1e1+λ2e2任一有且只有一对[微思考]定理中的“不共线”是否可以去掉?平面内的任一向量都能用e1,e2唯一表示吗?提示:不能去掉“不共线”,两个共线向量不能表示平面内的任一向量,不能作为基底.平面内任一向量都能用两个确定的不共线的e1,e2表示,且这样的表示是唯一的.(二)基本知能小试1.判断正误:(1)平面内任意两个向量都可以作为平面内所有向量的一个基底.()(2)零向量可以作为基向量.()(3)若e1,e2是同一平面内两个不共线向量,则λ1e1+λ2e2(λ1,λ2为实数)可以表示该平面内所有向量.()2.若e1,e2是平面内的一个基底,则下列向量能作为平面向量的基底的是()A.e1-e2,e2-e1B.2e1-e2,e1-12e2C.2e2-3e1,6e1-4e2D.e1+e2,e1-e2答案:D××√3.如图所示,向量OA―→可用向量e1,e2表示为________.答案:4e1+3e24.若向量e1,e2不共线,实数x,y满足(3x-4y)e1+(2x-3y)e2=6e1+3e2,则x-y的值为________.答案:3题型一对平面向量基本定理的理解【学透用活】(1)基底不唯一,只要是同一平面内的两个不共线向量都可以作为基底.同一非零向量在不同基底下的分解式是不同的.(2)基底给定时,分解形式唯一.λ1,λ2是被a,e1,e2唯一确定的数值.(3){e1,e2}是同一平面内所有向量的一个基底,则当a与e1共线时,λ2=0;当a与e2共线时,λ1=0;当a=0时,λ1=λ2=0.(4)由于零向量与任何向量都是共线的,因此零向量不能作为基底中的向量.[典例1](多选)如图,设O是平行四边形ABCD两对角线的交点,有下列向量组,可作为该平面内的其他向量基底的是()A.AD―→与AB―→B.DA―→与BC―→C.CA―→与DC―→D.OD―→与OB―→[...