1.2.2同角三角函数关系(1).pptVIP免费

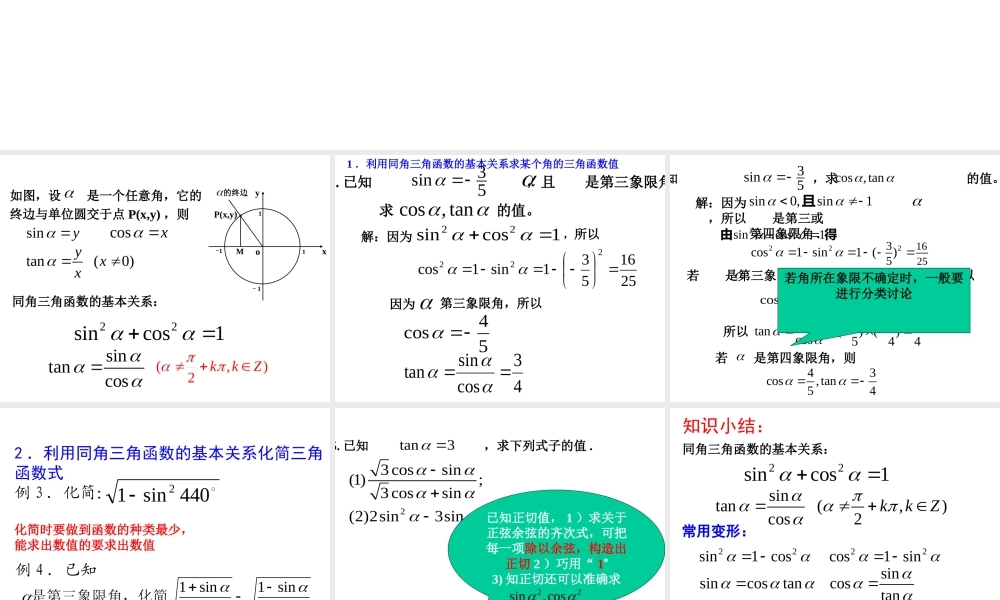
如图，设是一个任意角，它的终边与单位圆交于点P(x,y)，则sinycosxtan(0)yxxxyoP(x,y)1-11-1的终边M22sincos1同角三角函数的基本关系：sintancos(,)2kkZ.已知，且是第三象限角3sin5cos,tan求的值。解：因为1cossin22，所以2516531sin1cos222第三象限角，所以因为54cos43cossintan1．利用同角三角函数的基本关系求某个角的三角函数值知，求的值。3sin5cos,tan解：因为，所以是第三或第四象限角.sin0,sin1且22sincos1由得222162535cos1sin1()若是第三象限角，则，所以cos0416255cos所以353sintan()()cos544若是第四象限角，则43cos,tan54若角所在象限不确定时，一般要进行分类讨论2．利用同角三角函数的基本关系化简三角函数式例3．化简：化简时要做到函数的种类最少，能求出数值的要求出数值440sin12例4．已知sin1sin1sin1sin1是第三象限角，化简tan35.已知，求下列式子的值.23cossin(1);3cossin(2)2sin3sincos.已知正切值，1）求关于正弦余弦的齐次式，可把每一项除以余弦，构造出正切2）巧用“1”3)知正切还可以准确求22sin,cos22sincos1同角三角函数的基本关系：sintan(,)cos2kkZ常用变形：22sin1cos22cos1sinsincostansincostan知识小结：212sincos(sincos)提高：1sincos,,cossin.842已知且求222sincos,sincos,sincos(sincos)12sincos(sincos)(sincos)4sincos之间都能互相转换，只要知道其中的一个值，就能求出其余式子的值。数学应用sin1cos1cossin求证：1cos0,sin0.注意：我们今后所见到的三角恒等式，除特殊注明的情况外，都是指两边都有意义情况下的恒等式。如本题中默认为：.0sincos1)cos1(sinsincos1cos1sin22结论得证）（（作差法）证法一.sincos1cos1sin,0sin,0cos1,sincos1)cos1(cos122又）（向证明）证法二（分析结论，逆