0514高二数学（选修-人教B版）-导数的几何意义-2PPT.pptxVIP免费

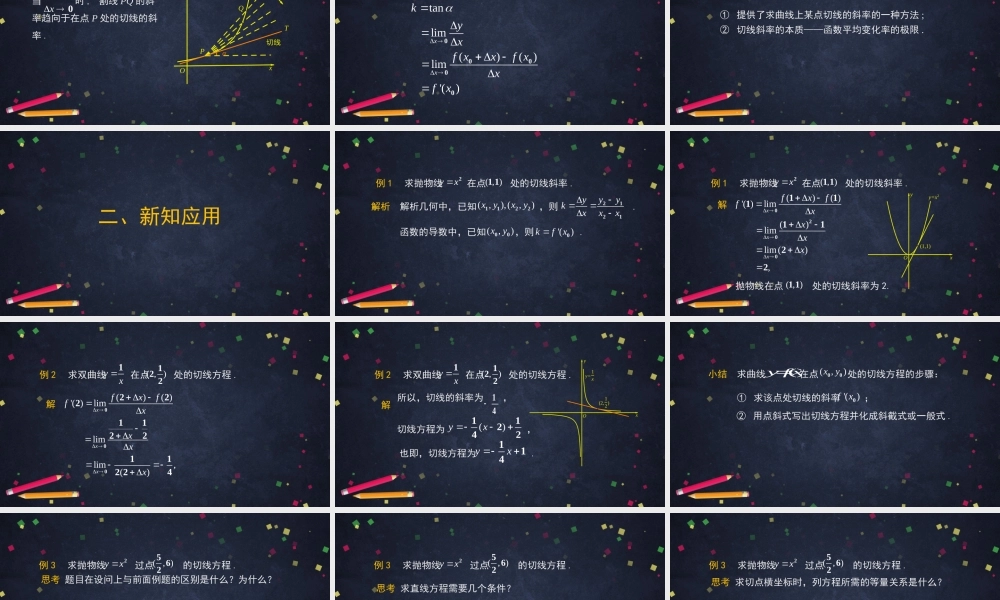
导数的几何意义高二年级数学主讲人：杨锦清华大学附属中学一、探究新知复习函数在处的瞬时变化率就称为函数在处的导数.()yfxxx0()yfxxx0问题通过函数的图象研究函数的性质是解决函数问题经常采用的方法，你能通过函数的图象研究函数的导数吗？()yfx复习计算函数在处导数的步骤：()yfxxx01.计算；()()yfxxfx002.计算；yx3.计算.limxyx0βMQPy=f(x)xyO观察图象曲线C是函数的图象,是曲线C上的任意一点,为P邻近一点,PQ为C的割线,PM//x轴,QM//y轴,β为PQ的倾斜角.()yfx(,)Pxy00(,)00Qxxyy,MPx观察图象,MQy因此，tanyx也即.PQykxβMQPy=f(x)xyO复习计算函数在处导数的步骤：()yfxxx01.计算；()()yfxxfx002.计算；yx3.计算.limxyx0思考对应怎样的图象变化？x0βMQPy=f(x)xyO观察图象请看当点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.α切线T割线QPy=f(x)xyO定义当点Q沿着曲线无限接近点P，即时,割线PQ有一个极限位置PT.我们把直线PT称为曲线在点P处的切线.x0α切线T割线QPy=f(x)xyO时，的变化对应了哪个几何量的变化？x0yx问题割线的倾斜角α切线T割线QPy=f(x)xyO概念当时,割线PQ的斜率趋向于在点P处的切线的斜率.x0α切线T割线QPy=f(x)xyOtanlim()()lim'()xxkyxfxxfxxfx00000理解概念切线的斜率k存在时，设切线的倾斜角为,理解概念导数的几何意义①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限.二、新知应用例1求抛物线在点处的切线斜率.yx2(,)11解析解析几何中，已知，则.(,),(,)xyxy1122yyykxxx2121函数的导数中，已知，则.(,)xy00'()kfx0例1求抛物线在点处的切线斜率.yx2(,)11解()()'()lim()limlim(),xxxfxffxxxx02001111122抛物线在点处的切线斜率为2.(,)11(1,1)y=x2Oxy例2求双曲线在点处的切线方程.yx1(,)122解()()'()limlimlim,()000222112211224xxxfxffxxxx解所以，切线的斜率为，14切线方程为，()yx11242也即，切线方程为.yx114例2求双曲线在点处的切线方程.yx1(,)122(2,12)y=1xyxO小结求曲线在点处的切线方程的步骤：()yfx(,)xy00①求该点处切线的斜率；'()fx0②用点斜式写出切线方程并化成斜截式或...