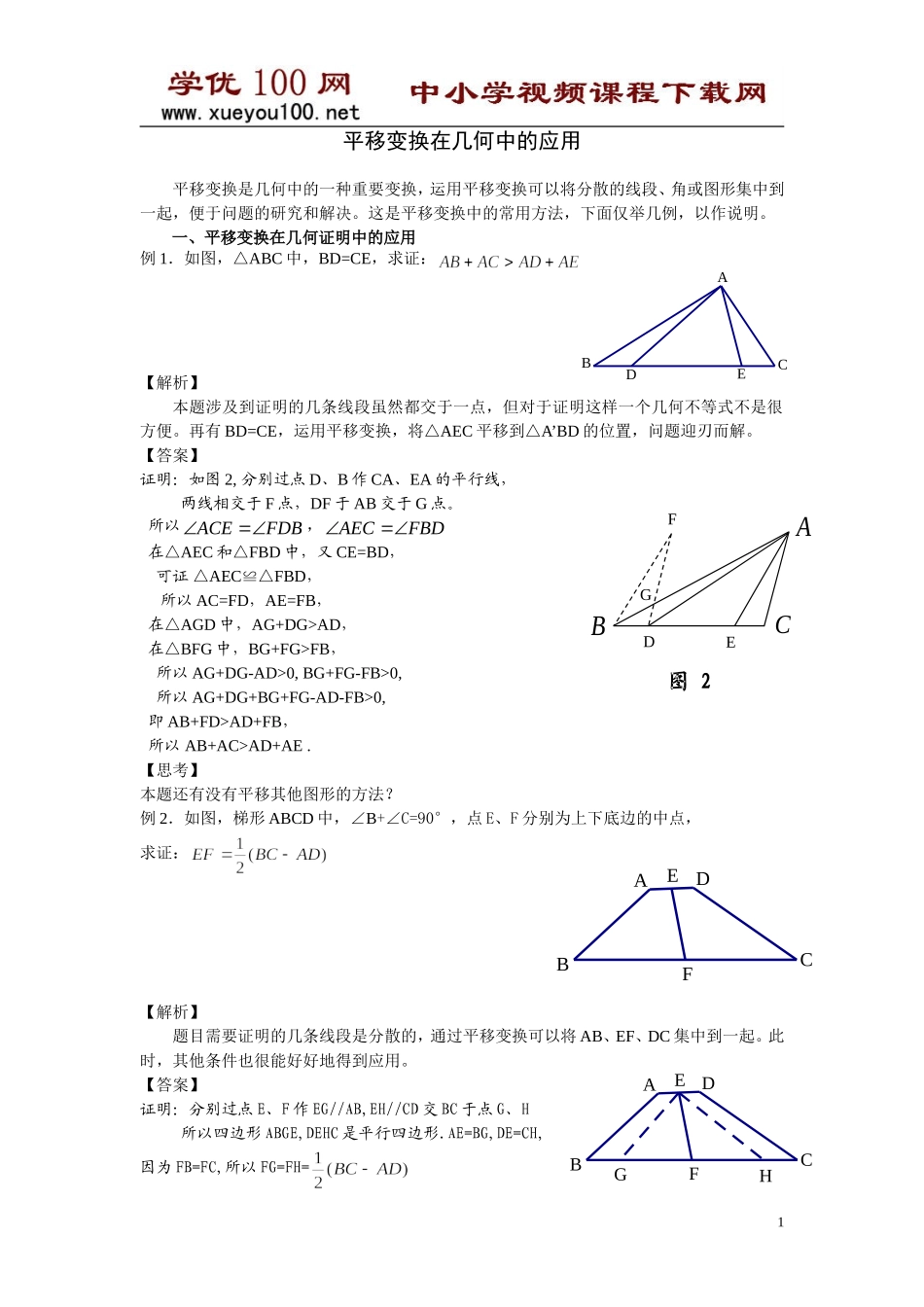
平移变换在几何中的应用平移变换是几何中的一种重要变换,运用平移变换可以将分散的线段、角或图形集中到一起,便于问题的研究和解决。这是平移变换中的常用方法,下面仅举几例,以作说明。一、平移变换在几何证明中的应用例1.如图,△ABC中,BD=CE,求证:【解析】本题涉及到证明的几条线段虽然都交于一点,但对于证明这样一个几何不等式不是很方便。再有BD=CE,运用平移变换,将△AEC平移到△A’BD的位置,问题迎刃而解。【答案】证明:如图2,分别过点D、B作CA、EA的平行线,两线相交于F点,DF于AB交于G点。所以ACEFDB,AECFBD在△AEC和△FBD中,又CE=BD,可证△AEC≌△FBD,所以AC=FD,AE=FB,在△AGD中,AG+DG>AD,在△BFG中,BG+FG>FB,所以AG+DG-AD>0,BG+FG-FB>0,所以AG+DG+BG+FG-AD-FB>0,即AB+FD>AD+FB,所以AB+AC>AD+AE.【思考】本题还有没有平移其他图形的方法?例2.如图,梯形ABCD中,∠B+∠C=90°,点E、F分别为上下底边的中点,求证:【解析】题目需要证明的几条线段是分散的,通过平移变换可以将AB、EF、DC集中到一起。此时,其他条件也很能好好地得到应用。【答案】证明:分别过点E、F作EG//AB,EH//CD交BC于点G、H所以四边形ABGE,DEHC是平行四边形.AE=BG,DE=CH,因为FB=FC,所以FG=FH=1EDCBAGFDEABCFEDCBAHGFEDCBA所以∠EGC=∠B,∠EHB=∠C,又∠B+∠C=90°,所以∠EGC+∠EHB=90°,∠GEH=90°所以△GEH是直角三角形.所以,EF=二、平移变换在几何作图中的应用例3.如图,河流的河岸AB与CD平行,点A、B表示两个村庄,现要在河上架桥,满足两个条件:(1)桥与河岸垂直;(2)A、B两个村庄之间的线路最短,请问桥应架在何处?【解析】不管桥设计在何处,A、B两个村庄之间的路程中总有一段是河岸间的距离,所以运用平移变换,将河“平移”,使村庄A或B恰好在河岸上。【答案】过点A作AA’垂直河岸,且使AA’长度等于河的宽度,连结交河岸于点C,过点C作CD垂直于河岸交河岸于点D,连结AD,则CD为桥的位置。【思考】如果A、B两个村庄之间有两条互相平行的小河,其他条件不变,桥的位置又该如何确定?例4.如图3,△ABC的三条中线分别为AD、BE、CF.在图3中利用图形变换画出并指明以AD、BE、CF的长度为三边长的一个三角形(保留画图痕迹);【解析】以三条中线为边长的三角形,显然要对这三条线段进行“重新组合”,手段就是平移变换。【答案】三、平移变换在几何计算中的应用例5.如图,六边形ABCDEF中,2BADCA'BA图3对角线已知FD=2...