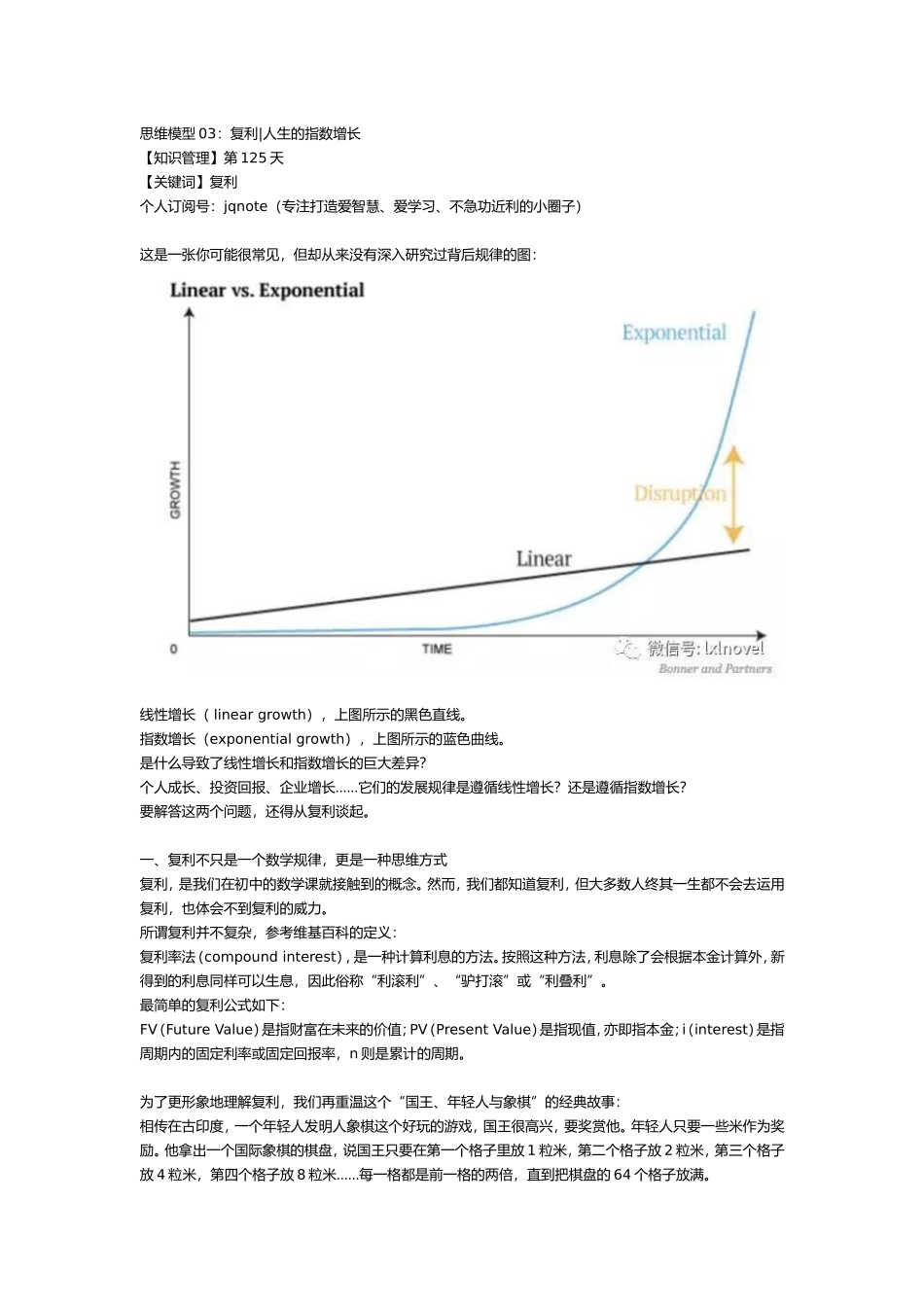
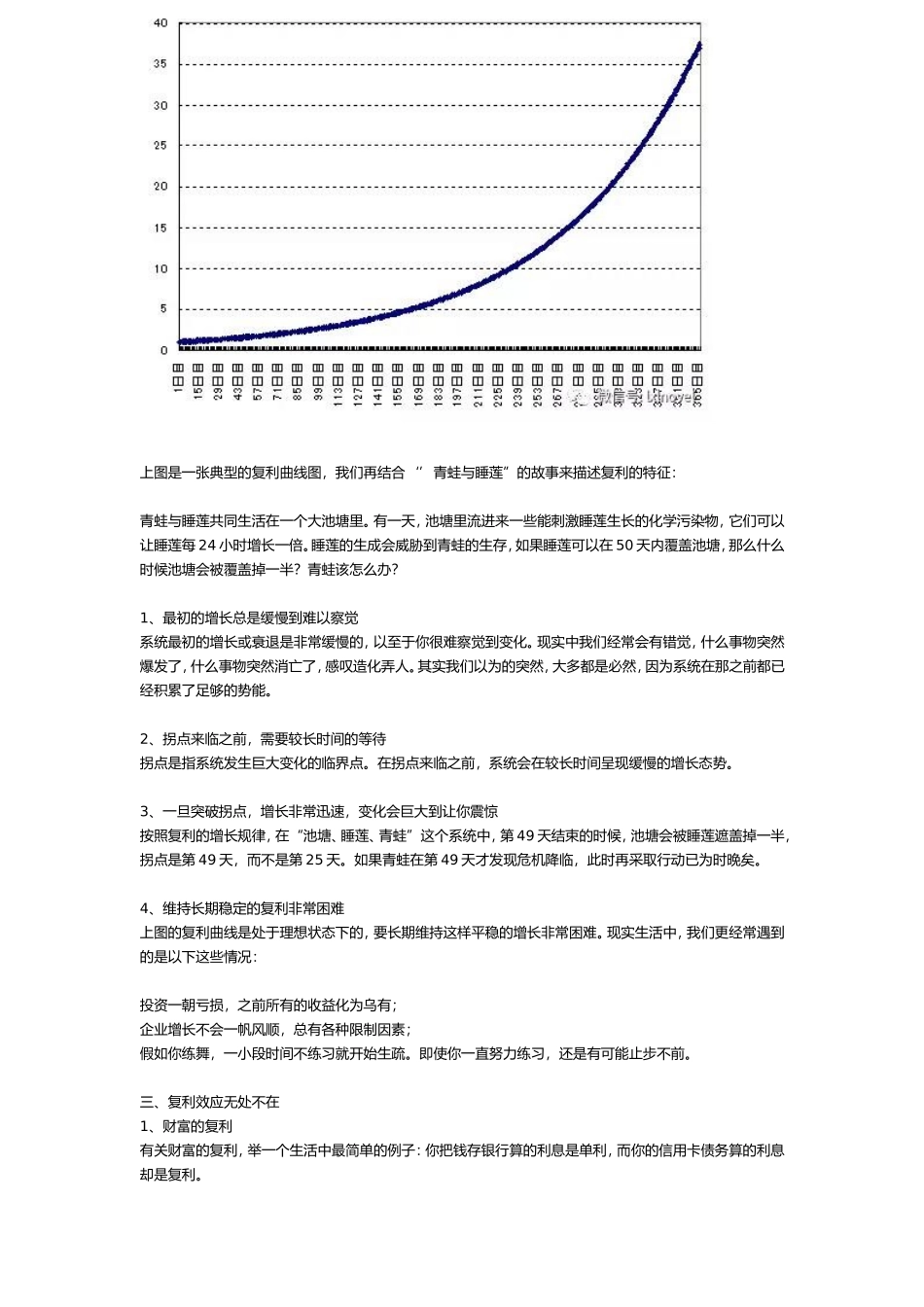
思维模型03:复利|人生的指数增长【知识管理】第125天【关键词】复利个人订阅号:jqnote(专注打造爱智慧、爱学习、不急功近利的小圈子)这是一张你可能很常见,但却从来没有深入研究过背后规律的图:线性增长(lineargrowth),上图所示的黑色直线。指数增长(exponentialgrowth),上图所示的蓝色曲线。是什么导致了线性增长和指数增长的巨大差异?个人成长、投资回报、企业增长……它们的发展规律是遵循线性增长?还是遵循指数增长?要解答这两个问题,还得从复利谈起。一、复利不只是一个数学规律,更是一种思维方式复利,是我们在初中的数学课就接触到的概念。然而,我们都知道复利,但大多数人终其一生都不会去运用复利,也体会不到复利的威力。所谓复利并不复杂,参考维基百科的定义:复利率法(compoundinterest),是一种计算利息的方法。按照这种方法,利息除了会根据本金计算外,新得到的利息同样可以生息,因此俗称“利滚利”、“驴打滚”或“利叠利”。最简单的复利公式如下:FV(FutureValue)是指财富在未来的价值;PV(PresentValue)是指现值,亦即指本金;i(interest)是指周期内的固定利率或固定回报率,n则是累计的周期。为了更形象地理解复利,我们再重温这个“国王、年轻人与象棋”的经典故事:相传在古印度,一个年轻人发明人象棋这个好玩的游戏,国王很高兴,要奖赏他。年轻人只要一些米作为奖励。他拿出一个国际象棋的棋盘,说国王只要在第一个格子里放1粒米,第二个格子放2粒米,第三个格子放4粒米,第四个格子放8粒米……每一格都是前一格的两倍,直到把棋盘的64个格子放满。按照年轻人的要求,国王能够兑现他的奖励吗?用复利的公式计算就可以得出结果:第1个小格子的米数1第2个小格子的米数2第3个小格子的米数4……第19个小格子的米数262144第20个小格子的米数524288……第64个小格子的米数9223372036854780000这是一个天文数字。我们可以对比下:2016年中国的粮食总产量12324.8亿斤,换算成米数也不够填满第64个小格子,更何况64个格子的米数相加的总量。世界上没有哪个国王可以兑现这个承诺。这就是复利的威力。二、复利的特征上图是一张典型的复利曲线图,我们再结合‘’青蛙与睡莲”的故事来描述复利的特征:青蛙与睡莲共同生活在一个大池塘里。有一天,池塘里流进来一些能刺激睡莲生长的化学污染物,它们可以让睡莲每24小时增长一倍。睡莲的生成会威胁到青蛙的生存,如果睡莲可以在50天内覆盖池塘,那么什么时...