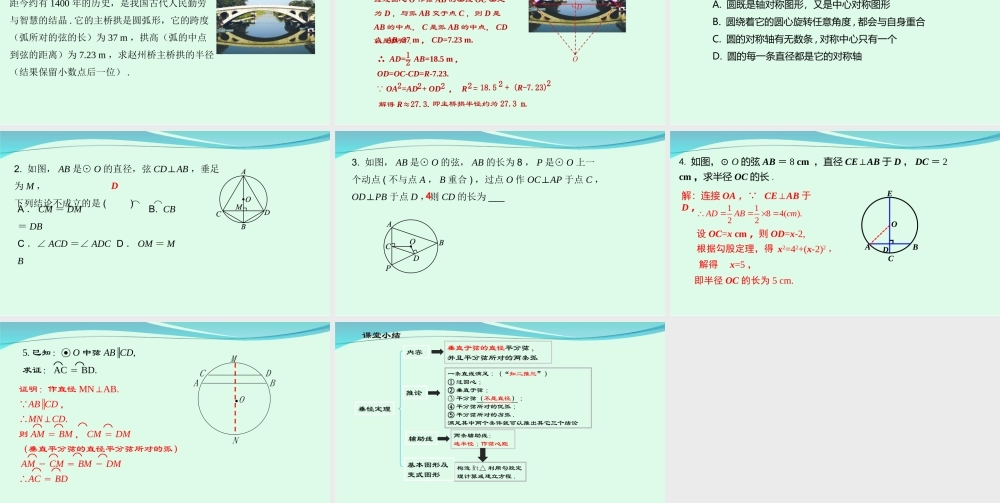
人教版九年级上册数学24.1.2垂直于弦的直径如图,1400多年前,我国隋代建造的赵州石拱桥主桥拱是圆弧形,它的跨度(弧所对的弦长)是37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(精确到0.1m).剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?通过探究可以发现,圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.●O求证:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.导引:要证明圆是轴对称图形,只需证明圆上任意一点关于直径所在直线(对称轴)的对称点也在圆上.·OA'ACDM证明:如图,设CD是⊙O的任意一条直径,A为⊙O上点C,D以外的任意一点.过点A作AA′⊥CD,交⊙O于点A′,垂足为M,连接OA,OA′.在△OAA′中, OA=OA′,∴△OAA′是等腰三角形.又 AA′⊥CD,∴AM=MA′.即CD是AA′的垂直平分线.·OA'ACDM这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A′,因此⊙O关于直线CD对称.例1下列说法中不正确的是()A.经过圆心的直线是圆的对称轴B.直径是圆的对称轴C.圆的对称轴有无数条D.当圆绕它的圆心旋转60°时,仍会与原来的圆重合D问题:如图,AB是⊙O的一条弦,直径CD⊥AB,垂足为E.你能发现图中有那些相等的线段和劣弧?为什么?·OABCDE线段:AE=BE弧:AC=BC,AD=BD⌒⌒⌒⌒理由如下:把圆沿着直径CD折叠时,根据前面的说理,点A与点B重合,AE与BE重合,AC和BC,AD与BD重合.⌒⌒⌒⌒垂径定理垂直于弦的直径平分弦,并且平分弦所对的两条弧.推导格式: CD是直径,CD⊥AB,∴AE=BE,⌒⌒AC=BC,⌒⌒AD=BD.·OABCDE平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.垂径定理推论推导格式: CD是直径,AE=BE,∴CD⊥AB,⌒⌒AC=BC,⌒⌒AD=BD.·OABCDE你还有其他的结论吗?你发现了什么??垂径定理的本质是:知二得三(1)一条直线过圆心(2)这条直线垂直于弦(3)这条直线平分不是直径的弦(4)这条直线平分不是直径的弦所对的优弧(5)这条直线平分不是直径的弦所对的劣弧例2赵州桥(如图)是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱的半径(结果保留小数点后一位).解:如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,...