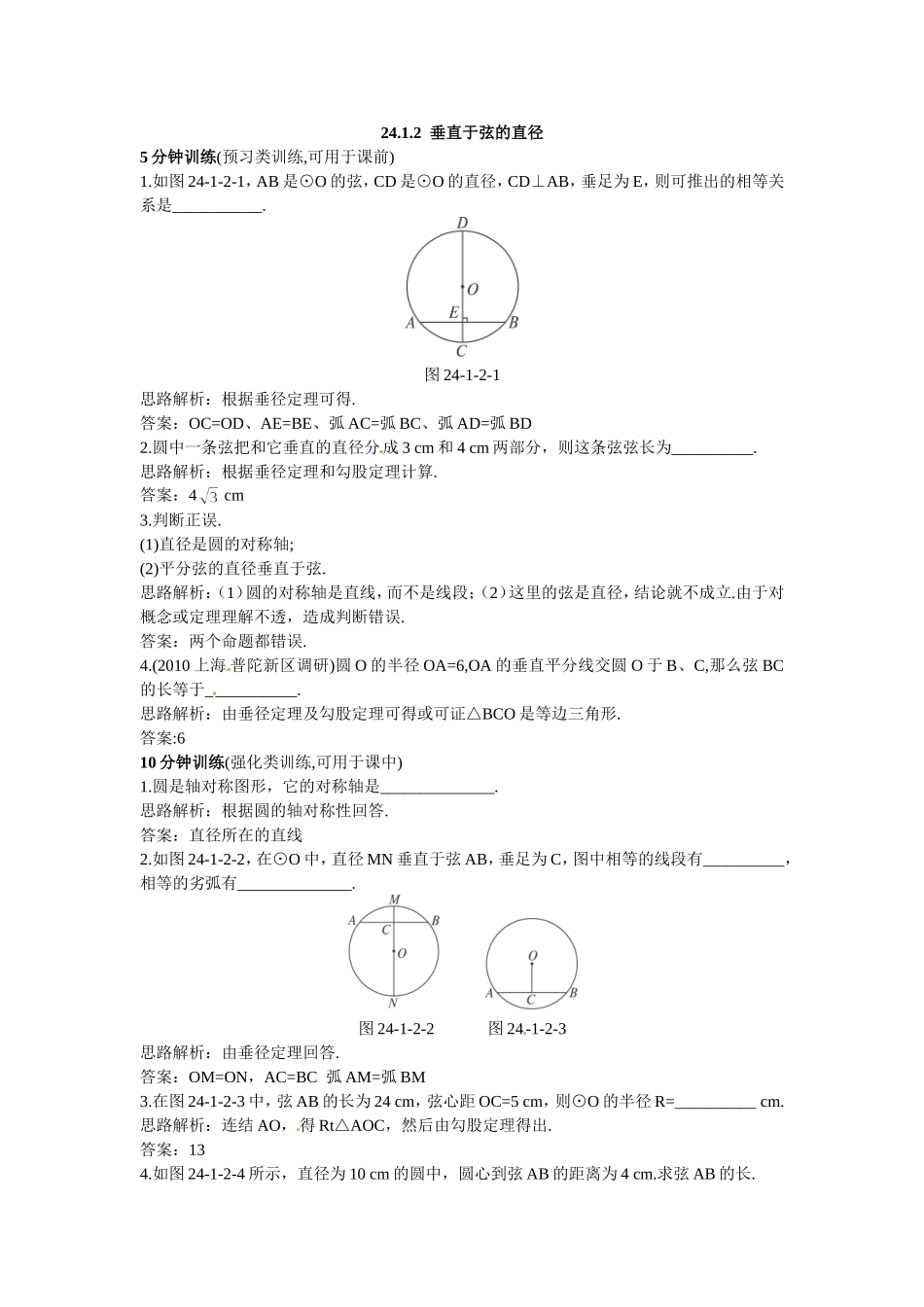
24.1.2垂直于弦的直径5分钟训练(预习类训练,可用于课前)1.如图24-1-2-1,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,则可推出的相等关系是___________.图24-1-2-1思路解析:根据垂径定理可得.答案:OC=OD、AE=BE、弧AC=弧BC、弧AD=弧BD2.圆中一条弦把和它垂直的直径分成3cm和4cm两部分,则这条弦弦长为__________.思路解析:根据垂径定理和勾股定理计算.答案:4cm3.判断正误.(1)直径是圆的对称轴;(2)平分弦的直径垂直于弦.思路解析:(1)圆的对称轴是直线,而不是线段;(2)这里的弦是直径,结论就不成立.由于对概念或定理理解不透,造成判断错误.答案:两个命题都错误.4.(2010上海普陀新区调研)圆O的半径OA=6,OA的垂直平分线交圆O于B、C,那么弦BC的长等于___________.思路解析:由垂径定理及勾股定理可得或可证△BCO是等边三角形.答案:610分钟训练(强化类训练,可用于课中)1.圆是轴对称图形,它的对称轴是______________.思路解析:根据圆的轴对称性回答.答案:直径所在的直线2.如图24-1-2-2,在⊙O中,直径MN垂直于弦AB,垂足为C,图中相等的线段有__________,相等的劣弧有______________.图24-1-2-2图24-1-2-3思路解析:由垂径定理回答.答案:OM=ON,AC=BC弧AM=弧BM3.在图24-1-2-3中,弦AB的长为24cm,弦心距OC=5cm,则⊙O的半径R=__________cm.思路解析:连结AO,得Rt△AOC,然后由勾股定理得出.答案:134.如图24-1-2-4所示,直径为10cm的圆中,圆心到弦AB的距离为4cm.求弦AB的长.图24-1-2-4思路分析:利用“圆的对称性”:垂直于弦的直径平分这条弦.由OM⊥AB可得OM平分AB,即AM=AB.连结半径OA后可构造Rt△,利用勾股定理求解.解:连结OA. OM⊥AB,∴AM=AB. OA=×10=5,OM=4,∴AM==3.∴AB=2AM=6(cm).快乐时光医学院的口试教授问一学生某种药每次口服量是多少?学生回答:“5克.”一分钟后,他发现自己答错了,应为5毫克,便急忙站起来说:“教授,允许我纠正吗?”教授看了一下表,然后说:“不必了,由于服用过量的药物,病人已经不幸在30秒钟以前去世了!”30分钟训练(巩固类训练,可用于课后)1.(安徽合肥模拟)如图24-1-2-5,⊙O的半径OA=3,以点A为圆心,OA的长为半径画弧交⊙O于B、C,则BC等于()A.3B.3C.D.图24-1-2-5图24-1-2-6思路解析:连结AB、BO,由题意知:AB=AO=OB,所以△AOB为等边三角形.AO垂直平分BC,所以BC=2×=3.答案:B2.(北京丰台模拟)如图24-1-2-6,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,OC=5cm,则OD的长是()A.3cmB.2.5cmC.2cmD....