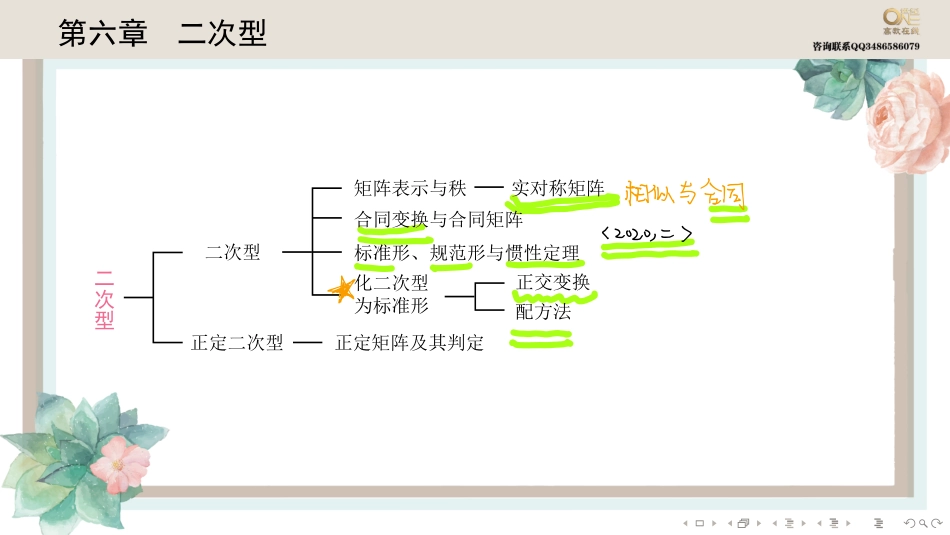
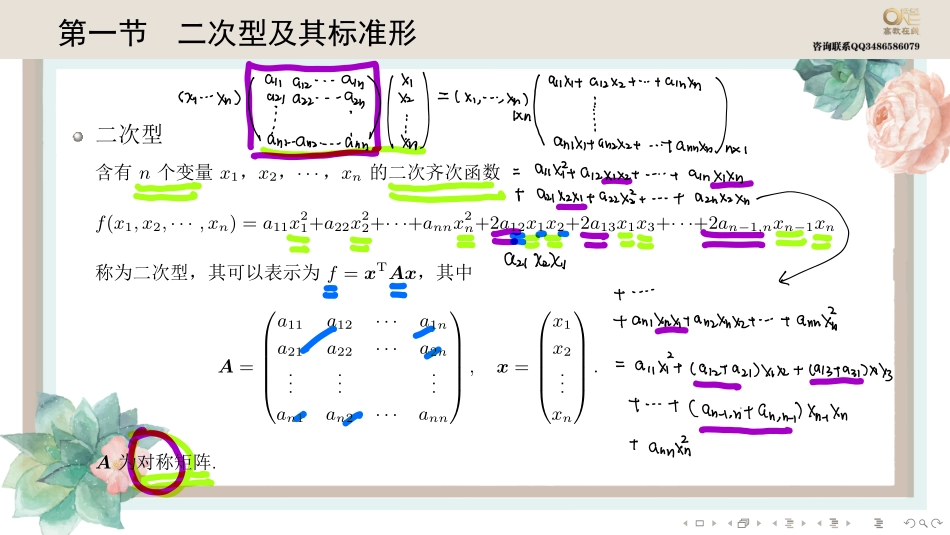
........������������������������������������������������������������������������相似与合同ㄑ2020⼆........����������������n���x1�x2�···�xn�������f(x1,x2,···,xn)=a11x21+a22x22+···+annx2n+2a12x1x2+2a13x1x3+···+2an−1,nxn−1xn������������f=xTAx���A=������a11a12···a1na21a22···a2n.........an1an2···ann������,x=������x1x2...xn������.A�����.anGn⼼加蠿fl鎚⼗以⼼⼀tanxniimamhtanzxzttannx.hnanxitazx.xzttamx.xntauxzx.tazzxittaznxzxr.az⽐I'DtamxnxtanzhnttamjanxitlantazDX.xz.tl1379引加3ttcamintan.nlhintanti.......xTAx=(x1,x2,···,xn)�������a11a12···a1na21a22···a2n.........an1an2···ann��������������x1x2...xn���������������������.�f=xTAx���A����f�����.����A�������f��.⼀唯⼀........�1..�A=�1122�.(1)��f(x)=xTAx�(2)��f(x)=xTAx��.�(1)f(x)=xTAx=(x1,x2)�1122��x1x2�TAX对于任何⼀个n阶知陈⽉都有意义可以算得⼀个⼆次⻬次函数也就是个⼆以型但该次型不是对称矩阵的秋不⼀定为run⼆次⻬次函数XhXHXzzxtnXRhX2t2Xxztzixi3xXzt2Xz𡷑型的秩2it了⼼⼆以⾦边炎⼜扣对称知⼰⻋f对应13⾔空nB21131to-75的秩为2.......�����A=�1ab2����a+b=3�����f(x1,x2)=xTAx=x21+3x1x2+2x22.���������������“��”�����.���f(x1,x2)=xTAx(A����)������f��������������.�A=(aij).���B=(bij)���bii=aii�bij=12(aij+aji)���B����������������f(x1,x2)=xTBx�B����f�����.���f�����B����.AaipÁuajiBÌAtAT2ton给刘向是up1ftipix的秩不能轻易下结论f的秗为1只有䃠⼼为对⼩阵时才可以.......�������������������������������������������������.�����f=n�i,j=1aijxixj(aij=aji)�������x=Py��f�����f=λ1y21+λ2y22+···+λny2n,��λ1�λ2�···�λn�f�����A=(aij)����.对何时为之标⼦矩阵f对应的浙东矩阵应为Ì⼼的⽌肚A凹成河胙⼆阴Pjp...