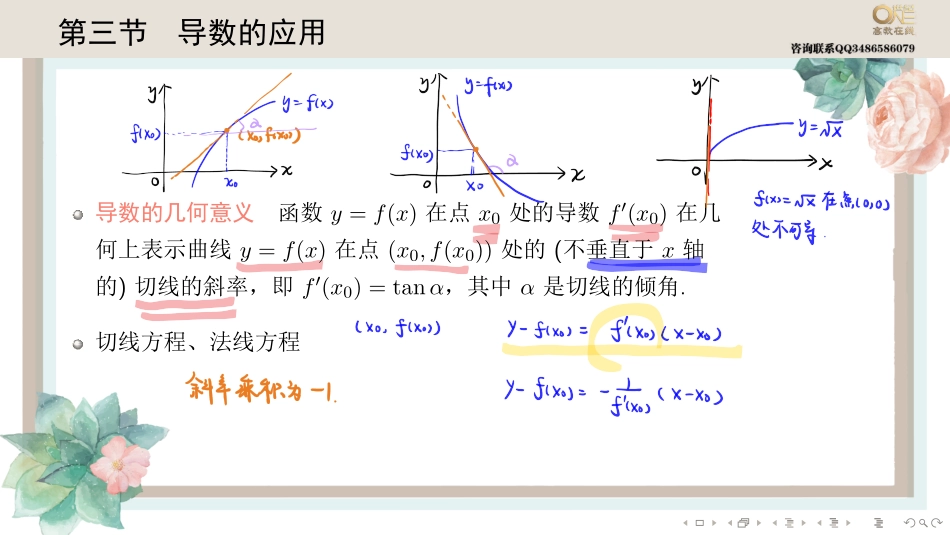
........第三节导数的应用导数的几何意义函数y=f(x)在点x0处的导数f′(x0)在几何上表示曲线y=f(x)在点(x0,f(x0))处的(不垂直于x轴的)切线的斜率,即f′(x0)=tanα,其中α是切线的倾角.切线方程、法线方程........例12..设周期函数f(x)在(−∞,+∞)内可导,周期为4.又limx→0f(1)−f(1−x)2x=−1,则曲线y=f(x)在点(5,f(5))处的切线的斜率为()(A)12.(B)0.(C)−1.(D)−2........曲率(数三不要求)曲率计算公式K=|y′′|[1+(y′)2]32.曲率圆与曲率半径(数三不要求)设曲线y=f(x)在点M(x,y)处的曲率为K(K̸=0).在点M处的曲线的法线上,在凹的一侧取一点D,使|DM|=1K=ρ.以D为圆心,ρ为半径作圆,所得圆为曲线在点M处的曲率圆.曲率圆的圆心D叫做曲线在点M处的曲率中心,曲率圆的半径ρ叫做曲线在点M处的曲率半径.........例13..曲线x=5t22+5,y=5t2+2t+6上对应于t=1的点处的曲率半径为........导数的物理应用导数的物理应用主要是变化率,温度变化率、体积变化率、速度等.路程关于时间的变化率,速率,带方向的话就是速度,v=dsdt,速度关于时间的变化率,加速度a=dvdt..例14..设有一个球体,其半径以0.01m/s的速率增加,求其半径为10m时,体积及表面积的增加率各为多少...............思考(2021,二)有一圆柱体,底面半径与高随时间变化的速度分别为2cm/s,−3cm/s,当底面半径为10cm,高为5cm时,圆柱体的体积与表面积随时间变化的速度分别为()(A)125πcm3/s,40πcm2/s.(B)125πcm3/s,−40πcm2/s.(C)−100πcm3/s,40πcm2/s.(D)−100πcm3/s,−40πcm2/s.����见讲义第三节同步习题.