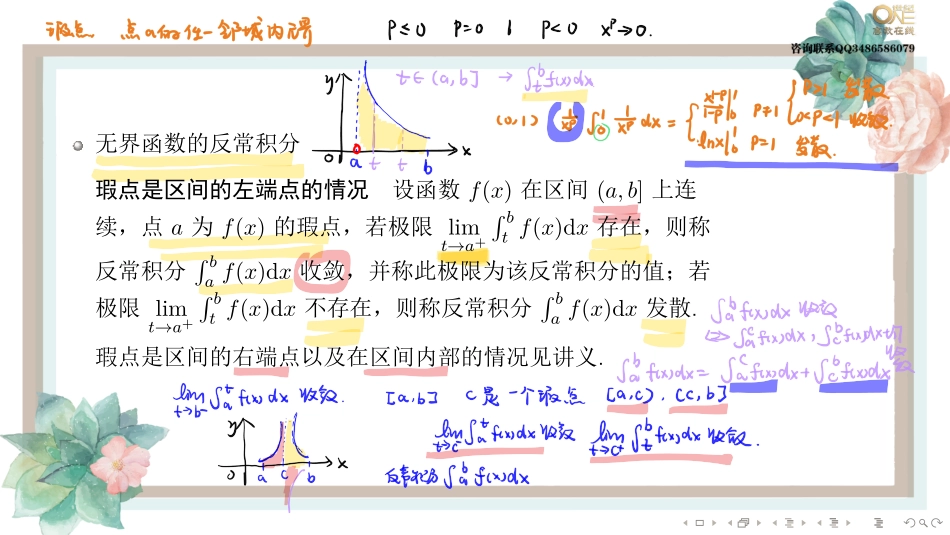
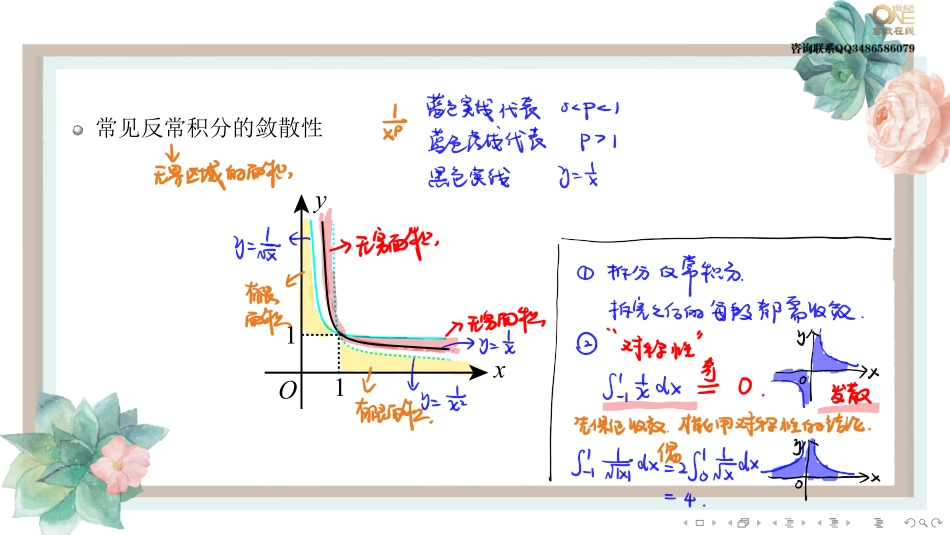
........第四节反常积分无穷限的反常积分设函数f(x)在区间[a,+∞)上连续,若极限limt→+∞∫taf(x)dx存在,则称反常积分∫+∞af(x)dx收敛,并称此极限为该反常积分的值;若极限limt→+∞∫taf(x)dx不存在,则称反常积分∫+∞af(x)dx发散.同理可定义∫b−∞f(x)dx的敛散性........无界函数的反常积分瑕点是区间的左端点的情况设函数f(x)在区间(a,b]上连续,点a为f(x)的瑕点,若极限limt→a+∫btf(x)dx存在,则称反常积分∫baf(x)dx收敛,并称此极限为该反常积分的值;若极限limt→a+∫btf(x)dx不存在,则称反常积分∫baf(x)dx发散.瑕点是区间的右端点以及在区间内部的情况见讲义........常见反常积分的敛散性yOx11........例15..计算∫+∞1arctanxx2dx........混合型反常积分我们称反常积分∫+∞af(x)dx收敛当且仅当所有这些区间上的瑕积分和无穷限的反常积分都收敛,否则称反常积分∫+∞af(x)dx发散.反常积分的几何意义与定积分一样,反常积分也可以表示面积(无界区域的面积)........无穷限反常积分的极限审敛法设函数f(x)在区间[a,+∞)上连续,f(x)≥0,并且存在常数p,使得limx→+∞xpf(x)=A.(i)若0≤A<+∞,p>1,则反常积分∫+∞af(x)dx收敛;(ii)若0
1.(B)a>1且b>1.(C)a<1且a+b>1.(D)a>1且a+b>1........视频:如何理解反常积分审敛法?都是比阶?b站@考研数学李艳芳����见讲义第四节同步习题.