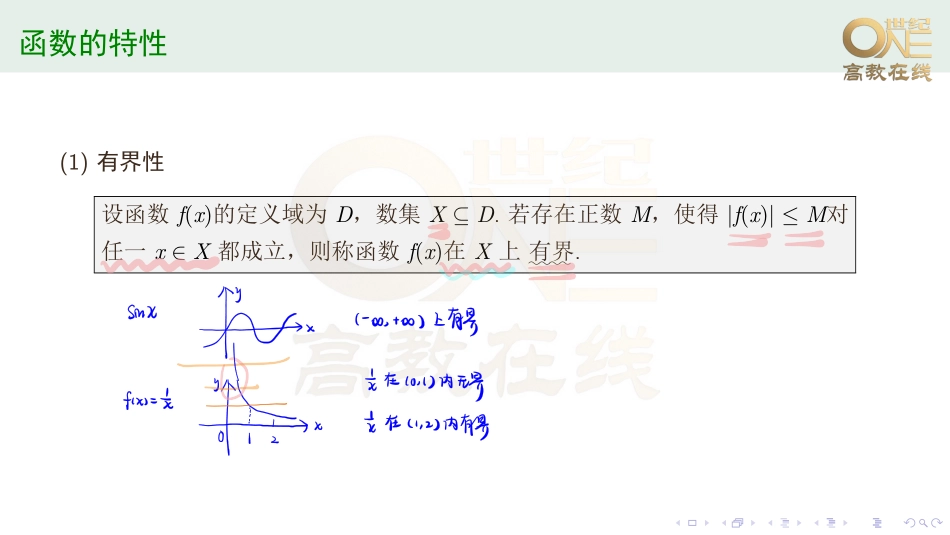
32天零基础小课堂�����������|��������......Day1:函数的特性与基本初等函数......函数的特性(1)有界性设函数f(x)的定义域为D,数集X⊆D.若存在正数M,使得|f(x)|≤M对任一x∈X都成立,则称函数f(x)在X上::有::界.......函数的特性(2)单调性设函数f(x)的定义域为D,区间I⊆D.若对于区间I上的任意两点x1及x2,当x1f(x2),则称函数f(x)在区间I上是::单::调:::减::少的.......函数的特性(3)奇偶性设函数f(x)的定义域D关于原点对称.若对于任一x∈D,f(−x)=f(x)恒成立,则称f(x)为:::偶::函::数.若对于任一x∈D,f(−x)=−f(x)恒成立,则称f(x)为:::奇::函::数.......函数的特性(4)周期性设函数f(x)的定义域为D.若存在一个正数l,使得对于任一x∈D有x±l∈D,且f(x+l)=f(x)恒成立,则称f(x)为:::周::期::函::数,l称为f(x)的::周::期.通常我们所说的周期函数的周期是指::最::小::正::周:::期.......基本初等函数•幂函数:y=xa(a是常数).•指数函数:y=ax(a>0且a̸=1).•对数函数:y=logax(a>0且a̸=1).•三角函数:y=sinx,y=cosx,y=tanx,y=cotx,y=secx,y=cscx.•反三角函数:y=arcsinx,y=arccosx,y=arctanx.............Day2:数列极限的定义......数列极限的定义定义设{xn}为一数列,若存在常数a,对于任意给定的ε>0(不论它多么小),总存在正整数N,使得当n>N时,不等式|xn−a|<ε都成立,则称常数::a:::为::数:::::::::列{xn}的::极::限,或者称::数::::::::列{xn}收:::敛:::于a,记为limn→∞xn=a,或xn→a(n→∞).ε−N定义:limn→∞xn=a等价于∀ε>0,∃正整数N,当n>N时,有|xn−a|<ε.......Day3:数列极限的性质......数列极限的性质(1)唯一性若数列{xn}收敛,则该极限唯一.(2)有界性若数列{xn}收敛,则该数列有界.(3)保号性若limn→∞xn=a,且a>0(或a<0),则存在正整数N,当n>N时,有xn>0(或xn<0).......数列极限的性质推论如果数列{xn}从某项起有xn≥0(或xn≤0),且limn→∞xn=a,那么a≥0(或a≤0).(4)收敛数列与其子数列之间的关系如果数列{xn}收敛于a,那么它的任一子数列也收敛,且极限也是a.由以上性质可知:如果数列{xn}有两个子数列收敛于不同的极限,那么数列{xn}是发散的.