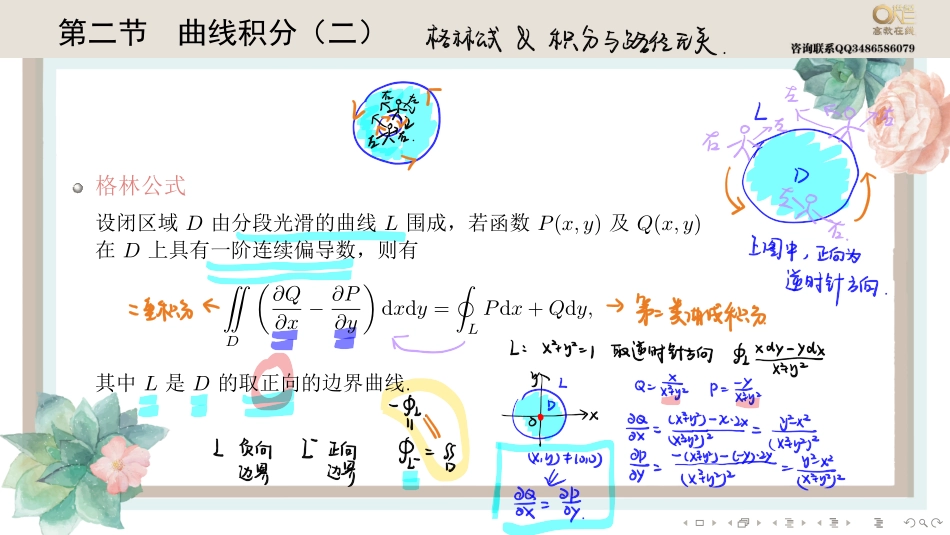
........第二节曲线积分(二)格林公式设闭区域D由分段光滑的曲线L围成,若函数P(x,y)及Q(x,y)在D上具有一阶连续偏导数,则有¨D(∂Q∂x−∂P∂y)dxdy=˛LPdx+Qdy,其中L是D的取正向的边界曲线.........例7..计算曲线积分´Lsin2xdx+2(x2−1)ydy,其中L是曲线y=sinx上从点(0,0)到点(π,0)的一段................例8..计算曲线积分I=¸Lxdy−ydx4x2+y2,其中L是以点(1,0)为中心,R为半径的圆周(R>1),取逆时针方向...............积分与路径无关的条件设D为平面中的单连通区域,函数P(x,y)和Q(x,y)在D上具有一阶连续偏导数,则以下条件相互等价.(1)对于D中任意分段光滑闭曲线C,都有¸CPdx+Qdy=0;(2)对于D中从点M1到点M2的任意两条分段光滑曲线L1,L2,都有ˆL1Pdx+Qdy=ˆL2Pdx+Qdy;(3)存在在D上具有一阶连续偏导数的函数u(x,y),使得d[u(x,y)]=Pdx+Qdy,u(x,y)被称为微分式Pdx+Qdy在D中的一个原函数;(4)在D中,恒有∂Q∂x=∂P∂y.........例9..若曲线积分´Lxdx−aydyx2+y2−1在区域D={(x,y)|x2+y2<1}内与路径无关,则a=........思考设Γ为简单光滑闭曲线,则曲线积分¸Γgrad[cos(x+y+z)+x2+y2+ez]·dr=........曲线积分的基本定理设F(x,y)=P(x,y)i+Q(x,y)j是平面区域D内的一个向量场.若P(x,y)与Q(x,y)都在D内连续,且存在一个数量函数f(x,y),使得F=∇f=∂f∂xi+∂f∂yj,则曲线积分´LF·dr在D内与路径无关,且ˆLF·dr=f(B)−f(A),其中L是位于D内起点为A,终点为B的任一分段光滑曲线.........例10..设函数f(x,y)满足∂f(x,y)∂x=(2x+1)e2x−y,且f(0,y)=y+1,Lt是从点(0,0)到点(1,t)的光滑曲线.计算曲线积分I(t)=´Lt∂f(x,y)∂xdx+∂f(x,y)∂ydy,并求I(t)的最小值...............全微分的原函数(1)P(x,y)dx+Q(x,y)dy为全微分的充分必要条件设区域D是一个单连通区域,若函数P(x,y)与Q(x,y)在D内具有一阶连续偏导数,则P(x,y)dx+Q(x,y)dy在D内为某一函数u(x,y)的全微分的充分必要条件是∂Q∂x=∂P∂y在D内恒成立.(2)全微分方程若一个微分方程能写成P(x,y)dx+Q(x,y)dy=0的形式,而P(x,y)dx+Q(x,y)dy为某一个函数u(x,y)的全微分,则上述方程称为全微分方程,u(x,y)=C是它的隐式通解,其中C为任意常数........已知某微分式,我们求其原函数u(x,y)的方法一般有如下三种:(1)折线法;(2)积分法;(3)凑微分法..例11..验证(yx+x2)dx+(lnx−2y)dy在右半平面x>0内是某一函数u(x,y)的全微分,并求这样的一个u(x,y)...............����见讲义第二节同步习题.