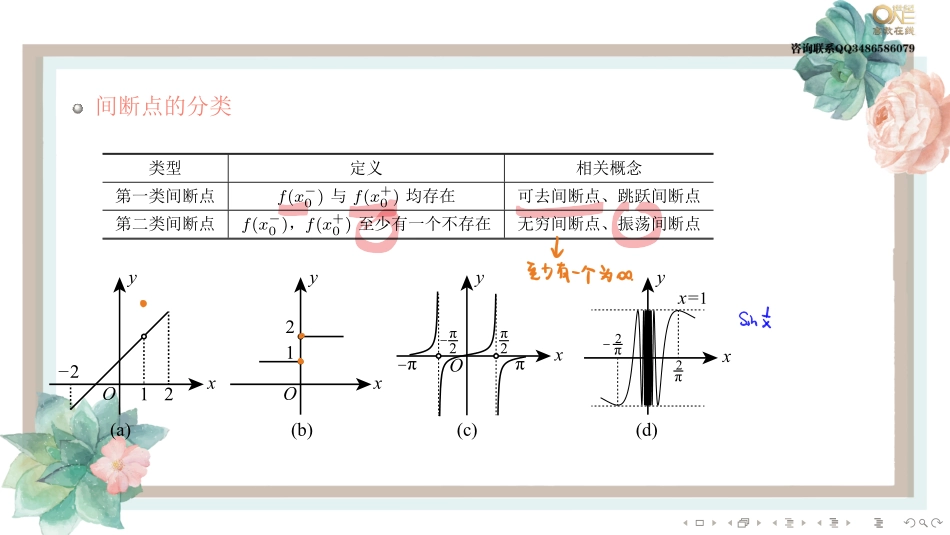
........第五节函数的连续性与间断点的类型连续的定义设函数y=f(x)在点x0的某一邻域内有定义,若limx→x0f(x)=f(x0),则称函数f(x)在点x0连续.ε−δ定义f(x)在点x0连续等价于∀ε>0,∃δ>0,当|x−x0|<δ时,有|f(x)−f(x0)|<ε.若limx→x−0f(x)=f(x−0)存在且等于f(x0),即f(x−0)=f(x0),则称函数f(x)在点x0左连续;若limx→x+0f(x)=f(x+0)存在且等于f(x0),即f(x+0)=f(x0),则称函数f(x)在点x0右连续........间断点的定义设函数f(x)在点x0的去心邻域内有定义.若f(x)满足下列情形之一:•在x=x0没有定义;•在x=x0有定义,limx→x0f(x)不存在或者limx→x0f(x)存在但limx→x0f(x)̸=f(x0),则称f(x)在x=x0不连续,x0为f(x)的间断点........间断点的分类类型定义相关概念第一类间断点f(x−0)与f(x+0)均存在可去间断点、跳跃间断点第二类间断点f(x−0),f(x+0)至少有一个不存在无穷间断点、振荡间断点yxOyxOyxOyx221(a)(b)(c)(d)12ππ2π2ππ2π2x=1........例13...设f(x)和φ(x)在(−∞,+∞)上有定义,f(x)为连续函数,且f(x)̸=0,φ(x)有间断点,则()(A)φ(f(x))必有间断点.(B)[φ(x)]2必有间断点.(C)f(φ(x))必有间断点.(D)φ(x)f(x)必有间断点........复合函数的连续性设函数y=f(g(x))是由函数u=g(x)与函数y=f(u)复合而成,x0的邻域U(x0)包含于复合函数f◦g的定义域.若函数u=g(x)在x=x0连续,且g(x0)=u0,而函数y=f(u)在u=u0连续,则复合函数y=f(g(x))在x=x0也连续.连续函数的和、差、积、商的连续性设函数f(x)和g(x)在点x0连续,则它们的和(差)f±g,积f·g及商fg(当g(x0)̸=0时)都在点x0连续.........例14..设函数f(x)=x2+1,|x|≤c,2|x|,|x|>c在(−∞,+∞)内连续,则c=.........例15..设函数f(x)=ln(1+ax3)x−arcsinx,x<0,6,x=0,eax+x2−ax−1xsinx4,x>0,问a为何值时,f(x)在x=0处连续;a为何值时,x=0是f(x)的可去间断点?.......����见讲义第五节同步习题.