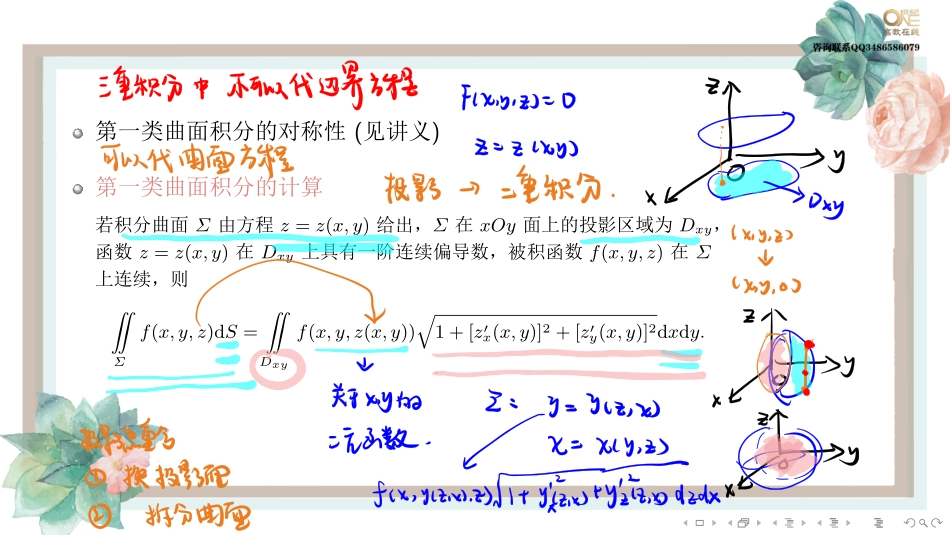
........第三节曲面积分(一)第一类曲面积分的定义设曲面Σ是光滑的,函数f(x,y,z)在Σ上有界.把Σ任意分成n小块∆Si(∆Si同时也代表第i块小曲面的面积),设(ξi,ηi,ζi)是∆Si上任意取定的一点,作乘积f(ξi,ηi,ζi)∆Si(i=1,2,···,n),并作和n∑i=1f(ξi,ηi,ζi)∆Si.若当各小块曲面的直径的最大值λ→0时,这和的极限总存在,且与曲面Σ的分法及点(ξi,ηi,ζi)的取法无关,则称此极限为函数f(x,y,z)在曲面Σ上对面积的曲面积分或第一类曲面积分,记作˜Σf(x,y,z)dS,即¨Σf(x,y,z)dS=limλ→0n∑i=1f(ξi,ηi,ζi)∆Si,其中f(x,y,z)叫做被积函数,Σ叫做积分曲面........第一类曲面积分的对称性(见讲义)第一类曲面积分的计算若积分曲面Σ由方程z=z(x,y)给出,Σ在xOy面上的投影区域为Dxy,函数z=z(x,y)在Dxy上具有一阶连续偏导数,被积函数f(x,y,z)在Σ上连续,则¨Σf(x,y,z)dS=¨Dxyf(x,y,z(x,y))√1+[z′x(x,y)]2+[z′y(x,y)]2dxdy.........例12..求抛物面壳z=12(x2+y2)(0≤z≤1)的质量,此壳的面密度为µ=z........第二类曲面积分的定义设Σ为光滑的有向曲面,函数R(x,y,z)在Σ上有界.把Σ任意分成n块小曲面∆Si(∆Si同时也代表第i块小曲面的面积),∆Si在xOy面上的投影为(∆Si)xy,(ξi,ηi,ζi)为∆Si上任意取定的一点,作乘积R(ξi,ηi,ζi)(∆Si)xy(i=1,2,···,n),并作和n∑i=1R(ξi,ηi,ζi)(∆Si)xy.若当各小块曲面的直径的最大值λ→0时,这和的极限总存在,且与曲面Σ的分法以及点(ξi,ηi,ζi)的取法无关,则称此极限为函数R(x,y,z)在有向曲面Σ上对坐标x,y的曲面积分,记作˜ΣR(x,y,z)dxdy,即¨ΣR(x,y,z)dxdy=limλ→0n∑i=1R(ξi,ηi,ζi)(∆Si)xy,其中R(x,y,z)叫做被积函数,Σ叫做积分曲面........右手直角坐标系下有向曲面、法向量以及方向余弦的关系曲面的表示方程曲面的侧法向量方向余弦z=z(x,y)上侧(−z′x,−z′y,1)cosγ>0下侧(z′x,z′y,−1)cosγ<0y=y(z,x)右侧(−y′x,1,−y′z)cosβ>0左侧(y′x,−1,y′z)cosβ<0x=x(y,z)前侧(1,−x′y,−x′z)cosα>0后侧(−1,x′y,x′z)cosα<0.......第二类曲面积分的计算设积分曲面Σ由方程z=z(x,y)给出,Σ在xOy面上的投影区域为Dxy,函数z=z(x,y)在Dxy上具有一阶连续偏导数,被积函数R(x,y,z)在Σ上连续.于是¨ΣR(x,y,z)dxdy=±¨DxyR(x,y,z(x,y))dxdy.若Σ取上侧,即cosγ>0,则上式右端取正号;若Σ取下侧,即cosγ<0,则上式右端取负号........第二类曲...