第五章第二节矩阵的相似与相似对角化（【公众号：最新考研资料】免费分享）.pdfVIP免费

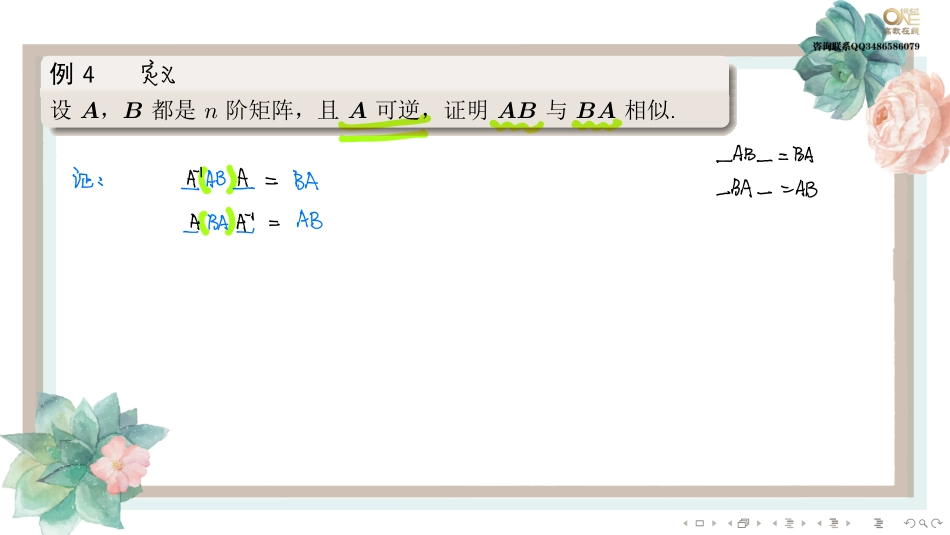
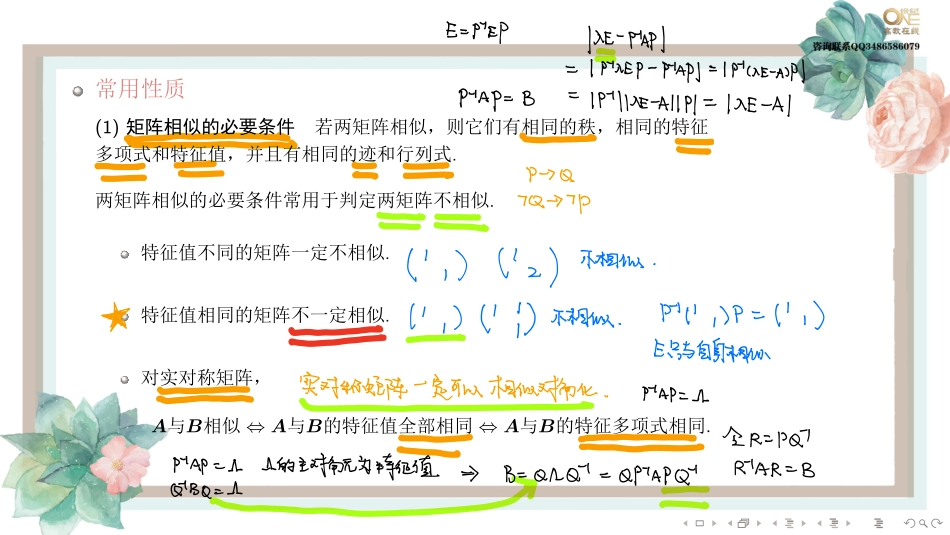
........�������������������A�B��n����������P��P−1AP=B���B�A�����������A�B��.�A����P−1AP���A�����������P���A��B�������.�P−1AP=Λ���Λ�������P��������AHMAP出A与对⻆矩阵⼏相似相似变换矩阵ARM⼼似六⼋P12122⼈P的刘向是为⽉的线we次的特征向是A121名⼈⼆2122-⼈以2⼼分AhAh⼀脑⼋⼩⼊⽔⼀⼊⽔AhiMainiln........�4..�A�B��n�����A�����AB�BA��.定义_AB_13A证ÀAB上BA13AABABAAB.......����(1)�������������������������������������������������.���������������������.�������������.�������������.�������A�B��⇔A�B��������⇔A�B��������.PETAHEiEP1MEppypjIPMEAPIPIAFBEIPMEAIIPFlMEApQ7Q77P1112不相似蘸li不相似MiP11上只与⾃身相似实对称矩阵⼀定可以相似对⻆化iAPltMAPin上的主对⻆⽆为特征价2AR⼆BGBQ⼆业之13Q⼉⼼Qpyp⼼全⼼⼼.......����(�)(2)������������.�A���B�B���C��A���C.�����A���������B���A��B��������.����A�B���������������Λ������������C����.(3)�A�������Λ��������P���P−1AP=Λ��A=PΛP−1.An=(PΛP−1)(PΛP−1)···(PΛP−1)����n�PΛP−1���========P−1P=EPΛnP−1.2014⼀⼆三利⽤对⻆矩阵过渡证明两矩阵相似幂pi相似啪化⼼似则⼼炽的幂零纪阵只需牌A的特么𡸜及特征向是tf........�5..�A�B�n�����A�B���E�n�������()(A)λE−A=λE−B.(B)A�B������������.(C)A�B����������.(D)�����t�tE−A�tE−B��.XA13由相似为相骂X相似为中轻值特么珦是相司X不⼀定能相似对⻆化解13PiAP⼆⼉BiBinR12均由特征问是构成AP㖄13冰⼼⼼671吢分6到1616到1367吢⾏15纰6到ˇ⾮巡必⼼从北到⼼⼼到䦻........�6..�3���A�����λ1=1�λ2=2�λ3=3�����������ξ1=����111�����ξ2=����124�����ξ3=����139��������β=����113����.(1)�β�ξ1�ξ2�ξ3�����(2)�Anβ(n����).20DMAP213151ctEAJPp...