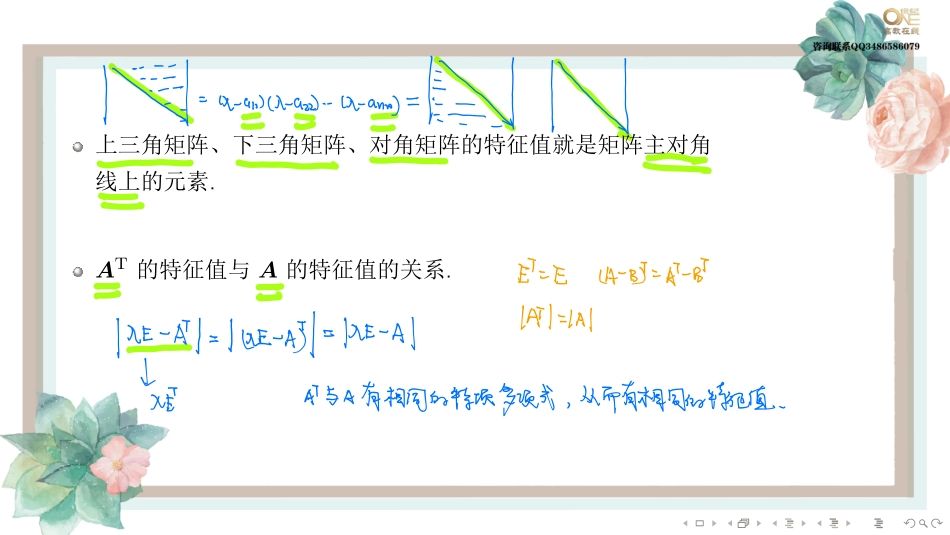
........�����������������������������������������������������������������������������������穆........��������������������A�n��������λ�n������α��Aα=λα��λ����A����.����α��A������λ�����.|λE−A|�λ�n�������f(λ)�����A������.f(λ)=|λE−A|=���������λ−a11−a12···−a1n−a21λ−a22···−a2n.........−an1−an2···λ−ann���������.X内Aiiijǚ你从cbgA2⼆⼋年AXno迫⼀⼊则义0特唨是蝌邹成说思in⼜是⼀吼120的⾮零特征㬀可辩解⼀逛⼀⽉江0得到A⼀忙不泄瞅.......��������������������������������.AT�����A�������.三三⼀⼆⽐们⼼幻⼀⽐am仨旭州1逖州旭州上让⼩叮我⼼刚测晶AT与⽉有相同的特项多项式从⽽有相同的特征值........�1..���A=����41−212a31−1����������������112������a=.A⽔⼊⼩解滩对应的特征值为⼊Iii詶滩㘅1鉫⼼hindas1.......����(1)�������������������n���A=(aij)�����λ1�λ2�···�λn��(i)λ1+λ2+···+λn=a11+a22+···+ann=tr(A).(ii)λ1λ2···λn=|A|.迹trueofAz阶情况ǙFǛǛÀǛǛTN⼋⼗⼋⼊⼗⼋⼊2t业常数项⼗⼋⼗⼋为⼼的系数.......������f(λ).f(λ)=|λE−A|=����������λ−a11−a12···−a1n−a21λ−a22···−a2n.........−an1−an2···λ−ann����������.f(λ)=(λ−λ1)(λ−λ2)···(λ−λn).A有⼏个特征值找常数项扣10EA1-A⼩洲找⼼的系数先从主对⻆线上选出以1个⼏⼆须主对⻆元均取出只能从LXauMazittam⾏列式与多项式出⼼业⼼的系数为⼀anazitann找⼼的系数点以2-灬⼼找常数项令⼊⼆0f以⼼的加⼊吣⼊⻔⼈叫外⼀⼩⼋⼋-⼼业1癿⼆⼋⼊2-M出各⾏琼之和相等⼆找⼀个特征值以及对应的特征向学.......����(�)(2)�λ�A������λk�Ak�����ϕ(λ)�ϕ(A)����(��ϕ(λ)=a0+a1λ+···+amλm�λ�����ϕ(A)=a0E+a1A+···+amAm���A����).(3)���λ�A�����α�λ������������������������α.��AkA+EA+kEAnA−1(A��)A∗(A��)���λkλ...