第二章作业选讲（2）√.pdfVIP免费

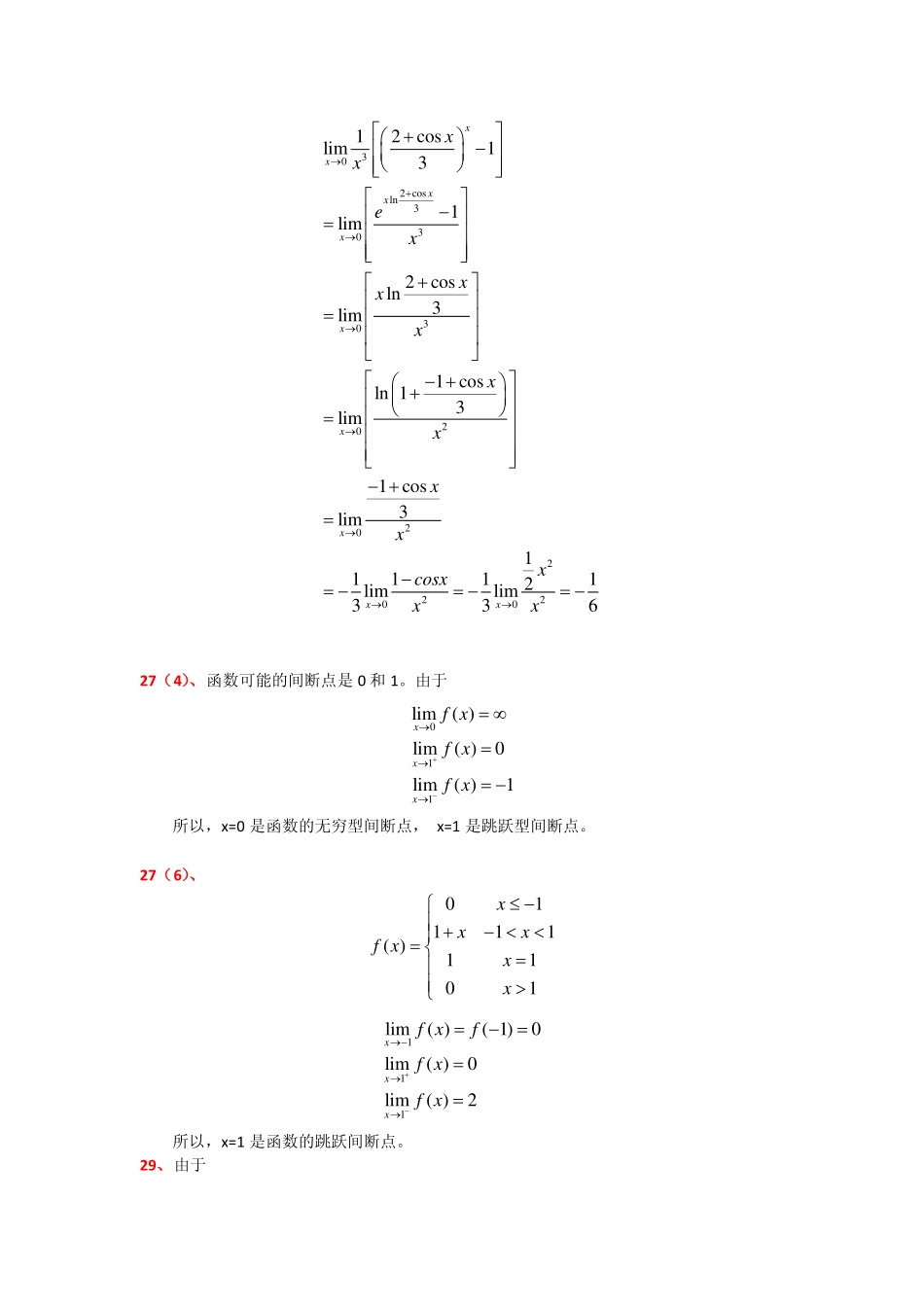
A组21（5）、方法一202001201lim111lim21lim3lim1eeexxxxxxxxxexexxxxee型方法二22120122012201220213lim1lim1lim1lim1xxxxxxxxxxxxeexxxxexeexeexeeeee型21（7）、方法一302cosln3303020202220012coslim131lim2cosln3lim1cosln13lim1cos3lim111112limlim336xxxxxxxxxxxxexxxxxxxxxcosxxx27（4）、函数可能的间断点是0和1。由于011lim()lim()0lim()1xxxfxfxfx所以，x=0是函数的无穷型间断点，x=1是跳跃型间断点。27（6）、01111()1101xxxfxxx111lim()(1)0lim()0lim()2xxxfxffxfx所以，x=1是函数的跳跃间断点。29、由于1100lim()lim()(1)2lim()1lim()(0)1xxxxfxfxffxfxf所以，函数在x=-1处连续，而在x=0处不连续。于是函数的连续区间是(3,0)和0,1。注：如果答案写成(3,0)0,1，老师觉得有点不妥当！30、证明令5()31fxxx，则f是[1,2]上的连续函数。由于，f130(2)3261250f根据连续函数的零点定理，(1,2)，使得()0f。于是即为满足根。31、证明令()sinfxxaxb，则f是实数域上的连续函数。首先，fabsin(1sin)0abaxbax如果fab0，那么a+b就是一个满足要求的正根。如果fab0，由于f0b0，连续函数的零点定理，(0,)ab，使得()0f。于是即为满足要求的正根。总之，方程x=sinaxb至少有一个不超过a+b的正根。32、证明令32()fxxbxcxd。由于323lim()lim1xxbcdfxxxxx，根据极限的定义，10M，当1xM时，()1fx，特别1(2)1fM。同理，20M，当2xM时，()1fx，特别2(2)1fM。在闭区间212,2MM应用连续函数的零点定理，即可知方程至少有一个实根。B组15、由于12xx，定义闭区间12,,22axbxAB，...