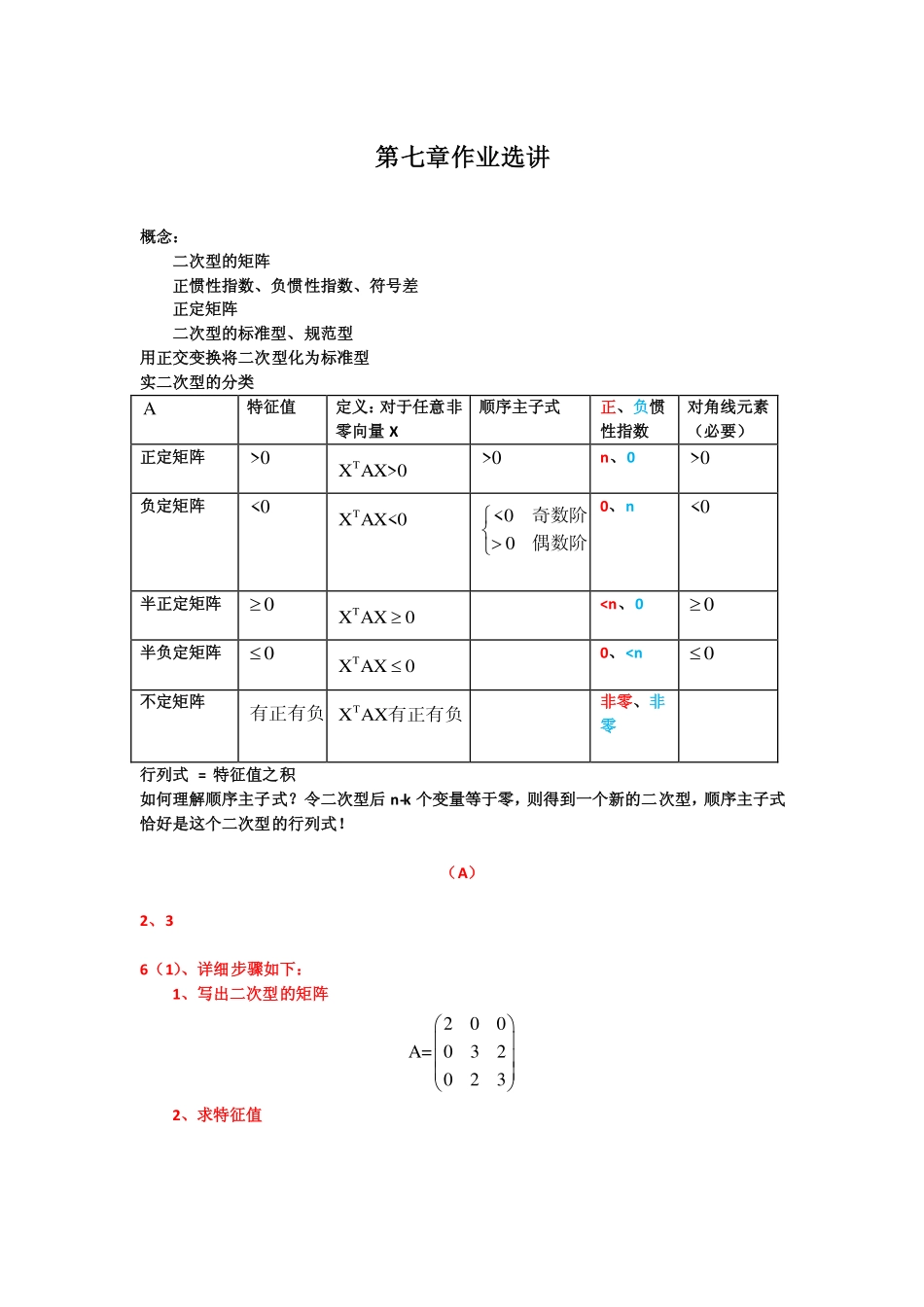
第七章作业选讲概念:二次型的矩阵正惯性指数、负惯性指数、符号差正定矩阵二次型的标准型、规范型用正交变换将二次型化为标准型实二次型的分类A特征值定义:对于任意非零向量X顺序主子式正、负惯性指数对角线元素(必要)正定矩阵>0TXAX>0>0n、0>0负定矩阵<0TXAX<0<00奇数阶偶数阶0、n<0半正定矩阵0TXAX001-3-211-21-71-71-130=1-34=<0-3410-41001注意这里不是求绝对值,是求阶行列式所以二次型为负定的。9、(B)3、(题目错误,修改为222123113(x,x,x)=(k+1)x+(k+2)x+(k+3)xf)正定的充要条件是特征值全部大于零,即+1>0,+2>0,+3>0kkk解不等式得>-1k。4、只需证明A的特征值全部大于0。证明:设是A的一个特征值,则32-2+4-3为32-2+4-3AAAE,即矩阵O的特征值,于是32()=-2+4-3=0f2'2'()=3-4+4,=-4-434<0,()>0ff故函数()f单调上升。又由于(0)=-3<0f,所以当()f的根只能大于0,即A的特征值全部大于0,A为正定矩阵。5、证明:用正交变换P将A化为标准型:12-1PAP=...n由于A为正定矩阵,>0(1in)i,于是-1-1-1-1=1+=P+=P+P=+P=+=+1>0nkkAEPEPPEPEE