第七章作业讲解√.pdfVIP免费

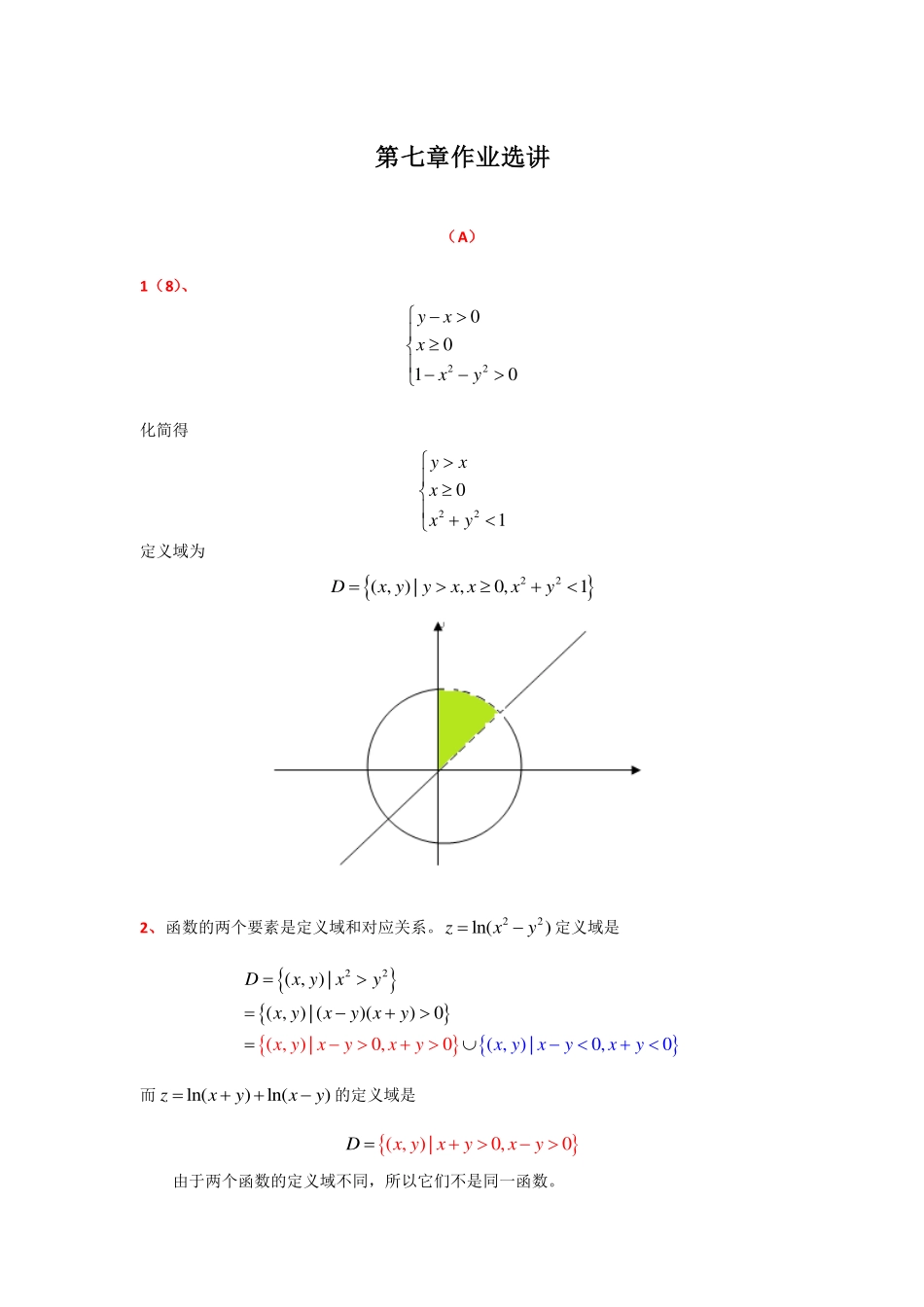
第七章作业选讲（A）1（8）、220010yxxxy化简得2201yxxxy定义域为22(,)|,0,1Dxyyxxxy2、函数的两个要素是定义域和对应关系。22ln()zxy定义域是22(,)|(,)|(,)|0,(,)|()000(),0xDxyxyxxyyxyxxyxyyxyyxy而ln()ln()zxyxy的定义域是(,)|0,0Dxyxyxy由于两个函数的定义域不同，所以它们不是同一函数。6、求下列函数的极限（1）22(,)(0,0)1lim()sinxyxyxy解运用两边夹定理，由于221()sinxyxyxyxyxy且(,)(0,0)(,)(0,0)(,)(0,0)limlimlim0xyxyxyxyxy所以22(,)(0,0)1lim()sin0xyxyxy（2）22(,)(1,0)ln()limyxyxexy解运用极限的四则运算和连续函数求极限的方法(,)(1,0)(,)(1,0)2222(,)(1,0)22(,)(1,0)(,)(1,0)limln()lnlim()ln()ln2limln21limlimyyyxyxyxyxyxyxexexexyxyxy（3）(,)(0,0)11limxyxyxy解运用无穷小量的因子代换12(,)(0,0)(,)(0,0)(,)(0,0)1111112limlimlim2xyxyxyxyxyxyxyxyxy（4）222222(,)(0,0)1coslimxyxyxyxye解运用无穷小量的因子代换22222222222222222(,)(0,0)(,)(0,0)(,)(0,0)111cos022limlimlim01xyxyxyxyxyxyxyxyxyxyexyee7、讨论函数(,)fxy的连续性244(,)(0,0)(,)0(,)(0,0)xyxyfxyxyxy解根据初等函数连续性的法则，(,)fxy在原点之外处处连续。以下用定义来检查函数在原点的连续性。由于22440,000444,0,000lim(,)limlim0001lim(,)lim2xyyyyxxyxxyfxyyyxfxyxx所以(,)(0,0)lim(,)xyfxy无极限，函数在原点不连续。8、求下列函数的偏导数（8）sin(1)arctanxyxzeyxy求''x(1,1)(1,1),yzz。解''x(1,1)1'1sin(1)arctansinarctan+(1)arctansinarctan14xxxxzexxexxxe''(1,1)11sinsincoscosyyyyyyzeyeyeyee9、求下列函数的偏导数（4）arctan1xyzxy求22222,,zzzxyxy。解2222222222222222222221(1)()11111111111210zxyyxyxxyxyxyyxyxyyyxyxyxyxyxzxxxzxy...