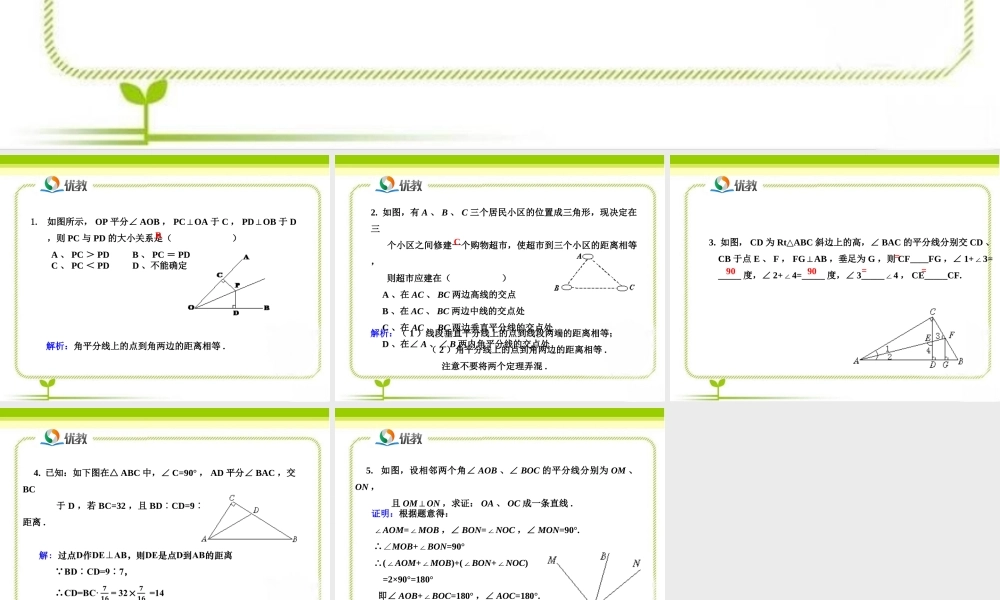
《角平分线》即时练习第2课时1.如图所示,OP平分∠AOB,PCOA⊥于C,PDOB⊥于D,则PC与PD的大小关系是()A、PC>PDB、PC=PDC、PC<PDD、不能确定解析:角平分线上的点到角两边的距离相等.B2.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在()A、在AC、BC两边高线的交点B、在AC、BC两边中线的交点处C、在AC、BC两边垂直平分线的交点处D、在∠A、∠B两内角平分线的交点处解析:(1)线段垂直平分线上的点到线段两端的距离相等;(2)角平分线上的点到角两边的距离相等.注意不要将两个定理弄混.C3.如图,CD为RtABC△斜边上的高,∠BAC的平分线分别交CD、CB于点E、F,FGAB⊥,垂足为G,则CF____FG,∠1+3=∠_____度,∠2+4=_____∠度,∠3_____4∠,CE_____CF.===90904.已知:如下图在△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BC=32,且BDCD=97∶∶,求:D到AB边的距离.5.如图,设相邻两个角∠AOB、∠BOC的平分线分别为OM、ON,且OM⊥ON,求证:OA、OC成一条直线.证明:根据题意得:∠AOM=∠MOB,∠BON=∠NOC,∠MON=90°.∴∠MOB+∠BON=90°∴(∠AOM+∠MOB)+(∠BON+∠NOC)=2×90°=180°即∠AOB+∠BOC=180°,∠AOC=180°.∴AO、OC成一条直线.结束