17.1 勾股定理第1课时.pptVIP免费

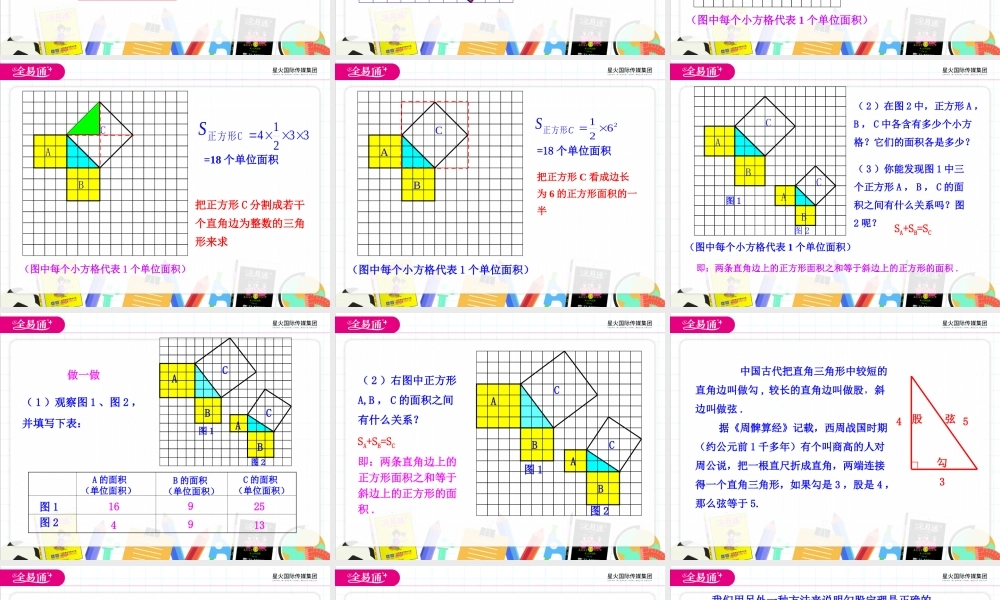
17.1勾股定理第1课时1.经历探索勾股定理及验证勾股定理的过程，了解勾股定理的探究方法及其内在联系.2.掌握勾股定理，并能运用勾股定理解决一些问题.学习目标学习目标这是1955年希腊为纪念一个数学学派发行的邮票.新课导入新课导入PRQ正方形P的面积正方形Q的面积正方形R的面积ABC916？怎么求SR的大小？有几种方案？如图，小方格的边长为1.知识讲解知识讲解勾股定理勾股定理知识点1知识点1PQCR用“补”的方法1494(43)225.SRPQCR用“割”的方法QSR14431225.ABC（图中每个小方格代表1个单位面积）（1）在图中，正方形A中含有个小方格，即A的面积是个单位面积.正方形B的面积是____个单位面积.正方形C的面积是_____个单位面积.99918探究勾股定理ABC（图中每个小方格代表1个单位面积）正方形CS14332把正方形C分割成若干个直角边为整数的三角形来求=18个单位面积ABC（图中每个小方格代表1个单位面积）正方形CS2162=18个单位面积把正方形C看成边长为6的正方形面积的一半ABCABC（图中每个小方格代表1个单位面积）图1图2（2）在图2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？（3）你能发现图1中三个正方形A，B，C的面积之间有什么关系吗？图2呢？SA+SB=SC即：两条直角边上的正方形面积之和等于斜边上的正方形的面积.ABC图1ABC图2（1）观察图1、图2，并填写下表：A的面积（单位面积）B的面积（单位面积）C的面积（单位面积）图1图2169254913做一做ABC图1ABC图2（2）右图中正方形A,B，C的面积之间有什么关系？SA+SB=SC即：两条直角边上的正方形面积之和等于斜边上的正方形的面积.中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股，斜边叫做弦.据《周髀算经》记载，西周战国时期（约公元前1千多年）有个叫商高的人对周公说，把一根直尺折成直角，两端连接得一个直角三角形，如果勾是3，股是4，那么弦等于5.345∟勾股弦人们还发现，在直角三角形中，勾是6，股是8，勾是5，股是12，弦一定是13，是不是所有的直角三角形都有这个性质呢？世界上许多数学家，先后用不同方法证明了这个结论.我国把它称为勾股定理.62=36,82=64,62+82=102102=100等等.52=25,122=144,52+122=132132=169弦一定是10；勾股定理如果直角三角形两直角边分别为a，b,斜边为c，那么222abc直角三角形两直角边的平方和等于斜边的平方.abc勾股弦abcabcbacabc用两种方法表示大正方形的面积:2)(ba2)21(4cbaabcbcbcbc...