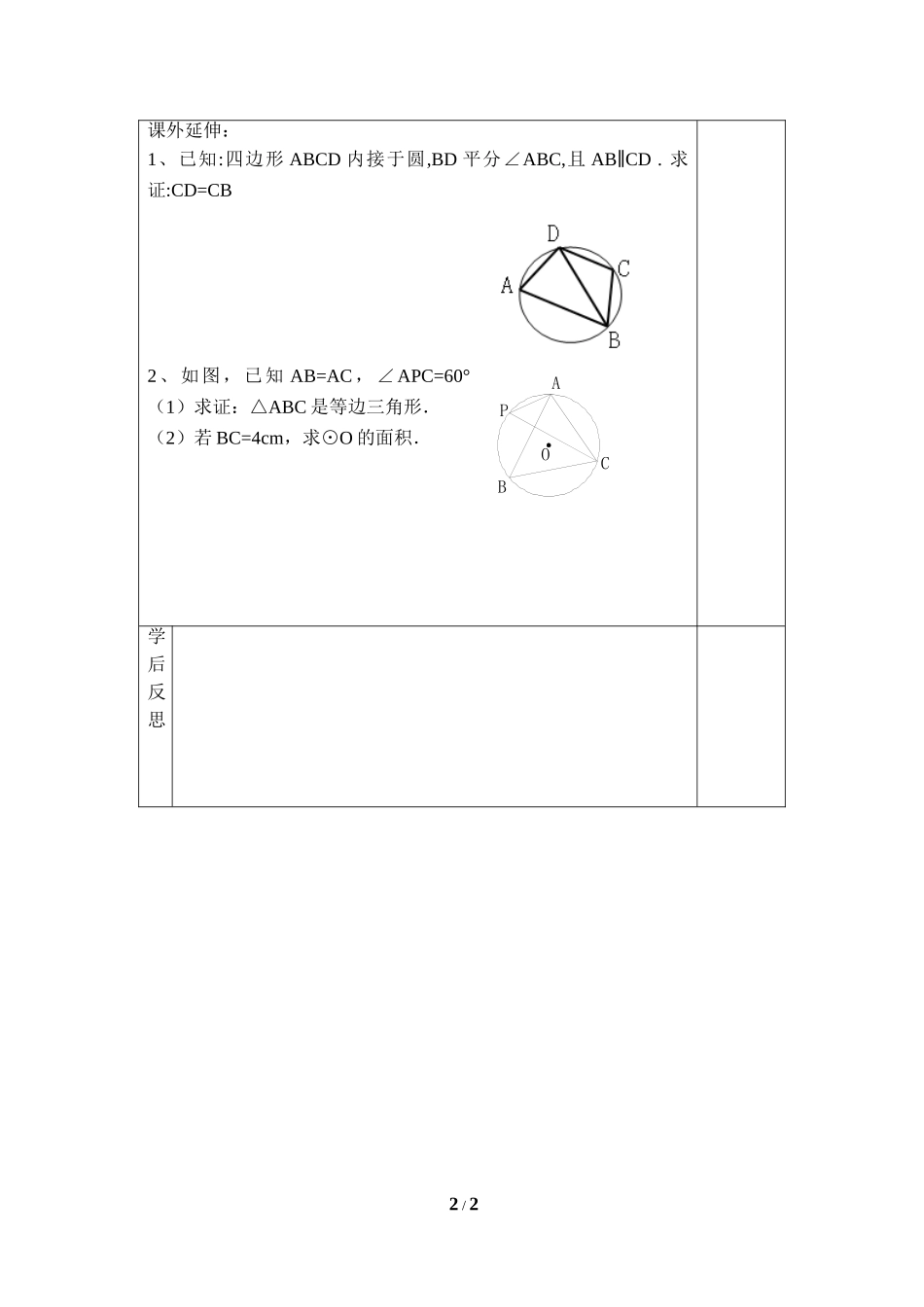
1/25.5确定圆的条件(2)学习目标:1.知道什么是圆内接多边形和多边形的外接圆。2.理解圆内接四边形的性质。3.会利用圆内接四边形的性质进行简单计算和证明。学习重点:圆内接四边形的性质的证明和应用。学习难点:圆内接四边形的性质的灵活应用。学习流程:一、复习引入:提问确定圆的条件及外接圆、外心、内接三角形概念。今天我们一起学习“圆内接四边形”的有关内容。二、展示目标,自学指导:认真阅读课本28页——30页内容,完成下列任务:(1)、什么是圆内接多边形?什么是多边形的外接圆?(2)、圆内接四边形有什么性质?怎么证明?(3)、先尝试自主完成例1,再看答案。(有困难可与同伴合作)(7分钟)三、检测自学效果:1、师生共同解决“议一议”中的问题。2、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A。3、课本30页随堂练习。四、课堂小结:本节课你有哪些收获?五、布置作业:必做题:课本30页习题5.8.自备自备2/2课外延伸:1、已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:CD=CB2、如图,已知AB=AC,∠APC=60°(1)求证:△ABC是等边三角形.(2)若BC=4cm,求⊙O的面积.学后反思OBACP