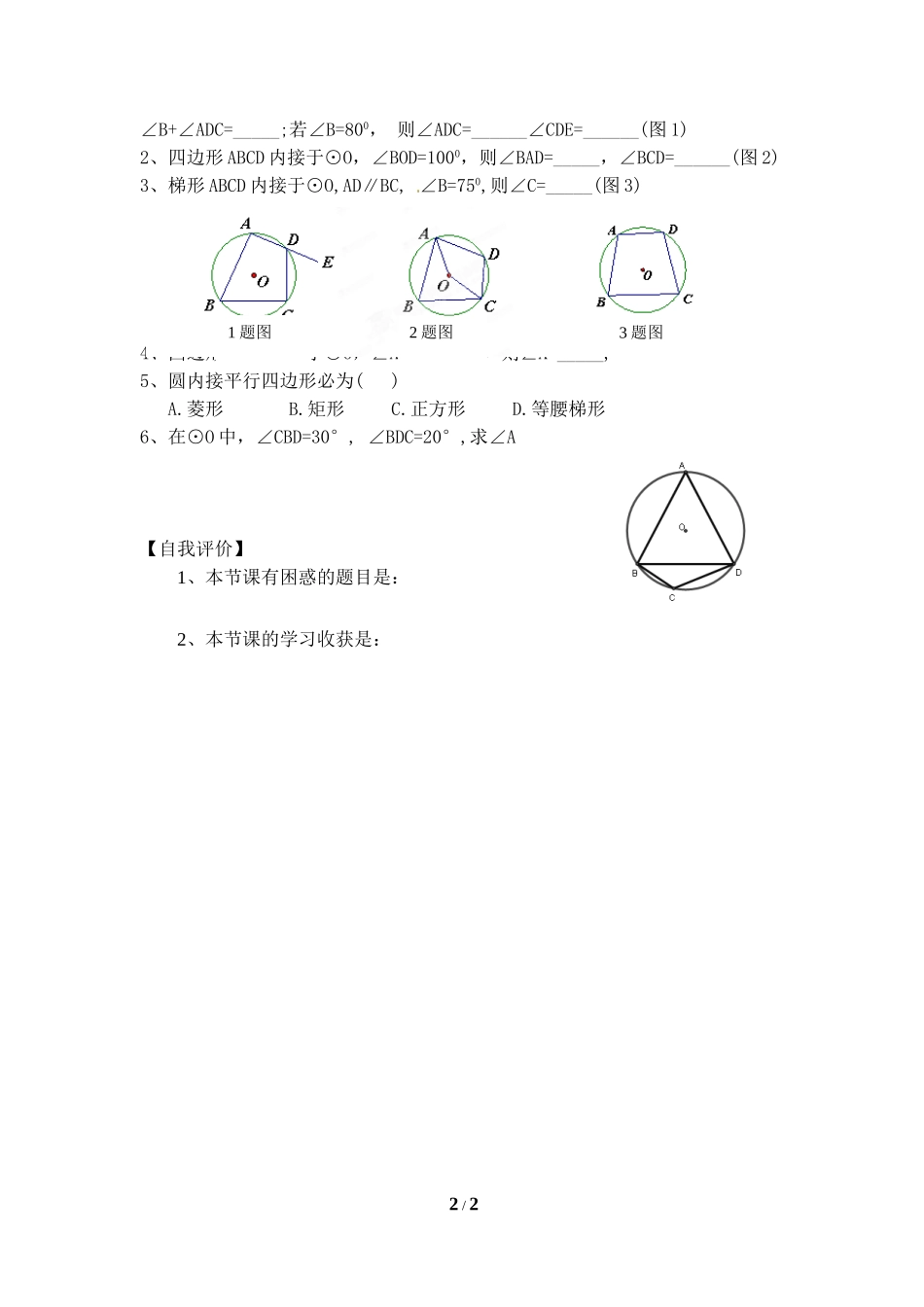
§5.5确定圆的条件(2)学习目标1.知道什么是圆内接多边形和多边形的外接圆。2.理解圆内接四边形的性质。3.会利用圆内接四边形的性质进行简单计算和证明。重点:圆内接四边形的性质的证明和应用。难点:圆内接四边形的性质的灵活应用一、引入新课1.如图(1),△ABC叫⊙O的_________三角形,⊙O叫△ABC的__圆。2.如上图(1),若的度数为1000,则∠BOC=__,∠A=___3.如图(2)四边形ABCD中,∠B与∠1互补,AD的延长线与DC所夹∠2=600,则∠1=___,∠B=___.二、探索交流阅读课本,解决下列问题如图(3),四边形ABCD的各顶点都在⊙O上,所以四边形ABCD是⊙O的____四边形,⊙O叫四边形ABCD的____圆.问题1什么叫圆内接多边形?多边形的外接圆呢?问题2你能解决下列问题吗?(1)如图3,在⊙O的内接四边形ABCD中,∠A与∠C,∠B与∠D分别是它的两组对角,∠A所对的弧是哪条弧?∠C所对的弧是哪条弧?(2)∠A与∠C所对的两条弧的度数之和是多少?由此你发现∠A与∠C有怎样的数量关系?∠B与∠D呢?得到定理:(3)如右图,延长BC到点E,得到∠DCE,∠DCE是四边形ABCD的一个外角,∠A称∠DCE的内对角,它两个的大小有什么关系?得到推论:三、练一练1、四边形ABCD内接于⊙O,则∠A+∠C=____,1/221EDCBAOCBAODABC图3图2图1OEDCBA∠B+∠ADC=_____;若∠B=800,则∠ADC=______∠CDE=______(图1)2、四边形ABCD内接于⊙O,∠BOD=1000,则∠BAD=_____,∠BCD=______(图2)3、梯形ABCD内接于⊙O,AD∥BC,∠B=750,则∠C=_____(图3)4、四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,5、圆内接平行四边形必为()A.菱形B.矩形C.正方形D.等腰梯形6、在⊙O中,∠CBD=30°,∠BDC=20°,求∠A【自我评价】1、本节课有困惑的题目是:2、本节课的学习收获是:2/21题图3题图2题图