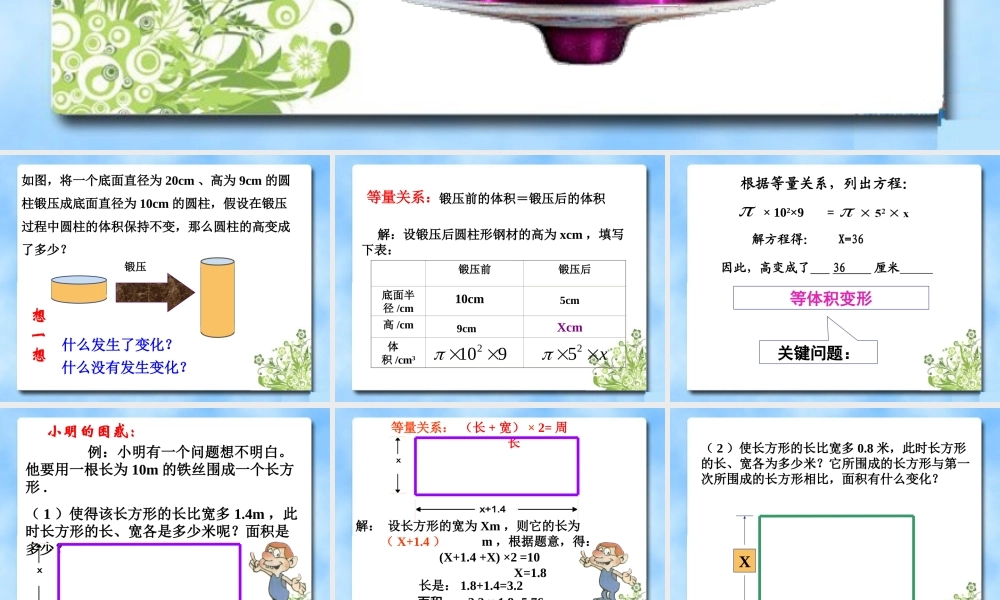
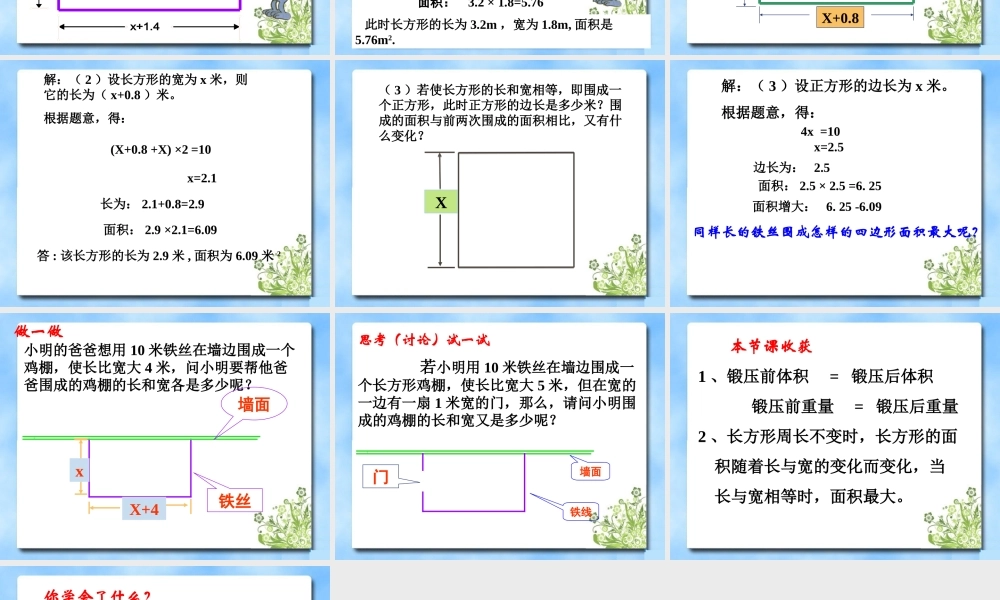
4.3应用一元一次方程(2)什么发生了变化?什么没有发生变化?如图,将一个底面直径为20cm、高为9cm的圆柱锻压成底面直径为10cm的圆柱,假设在锻压过程中圆柱的体积保持不变,那么圆柱的高变成了多少?想一想锻压解:设锻压后圆柱形钢材的高为xcm,填写下表:锻压前锻压后底面半径/cm高/cm体积/cm310cm5cm9cmXcm等量关系:锻压前的体积=锻压后的体积25x2109根据等量关系,列出方程:解方程得:X=36因此,高变成了36厘米等体积变形关键问题:=×102×9例:小明有一个问题想不明白。他要用一根长为10m的铁丝围成一个长方形.(1)使得该长方形的长比宽多1.4m,此时长方形的长、宽各是多少米呢?面积是多少?小明的困惑:xx+1.4解:设长方形的宽为Xm,则它的长为m,根据题意,得:(X+1.4+X)×2=10X=1.8长是:1.8+1.4=3.2此时长方形的长为3.2m,宽为1.8m,面积是5.76m2.等量关系:(长+宽)×2=周长(X+1.4)面积:3.2×1.8=5.76xx+1.4(2)使长方形的长比宽多0.8米,此时长方形的长、宽各为多少米?它所围成的长方形与第一次所围成的长方形相比,面积有什么变化?XX+0.8解:(2)设长方形的宽为x米,则它的长为(x+0.8)米。根据题意,得:(X+0.8+X)×2=10x=2.1长为:2.1+0.8=2.9面积:2.9×2.1=6.09答:该长方形的长为2.9米,面积为6.09米2(3)若使长方形的长和宽相等,即围成一个正方形,此时正方形的边长是多少米?围成的面积与前两次围成的面积相比,又有什么变化?X4x=10x=2.5边长为:2.5面积:2.5×2.5=6.25解:(3)设正方形的边长为x米。根据题意,得:面积增大:6.25-6.09同样长的铁丝围成怎样的四边形面积最大呢?小明的爸爸想用10米铁丝在墙边围成一个鸡棚,使长比宽大4米,问小明要帮他爸爸围成的鸡棚的长和宽各是多少呢?铁丝墙面xX+4做一做思考(讨论)试一试若小明用10米铁丝在墙边围成一个长方形鸡棚,使长比宽大5米,但在宽的一边有一扇1米宽的门,那么,请问小明围成的鸡棚的长和宽又是多少呢?门墙面铁线1、锻压前体积=锻压后体积锻压前重量=锻压后重量2、长方形周长不变时,长方形的面积随着长与宽的变化而变化,当长与宽相等时,面积最大。本节课收获审设把有关的量用含有未知数的代数式表示列根据等量关系列出方程。解解方程答审清题意检验作答应用方程解决问题的一般步骤:你学会了什么?