6.1 平方根（第2课时）.pptxVIP免费

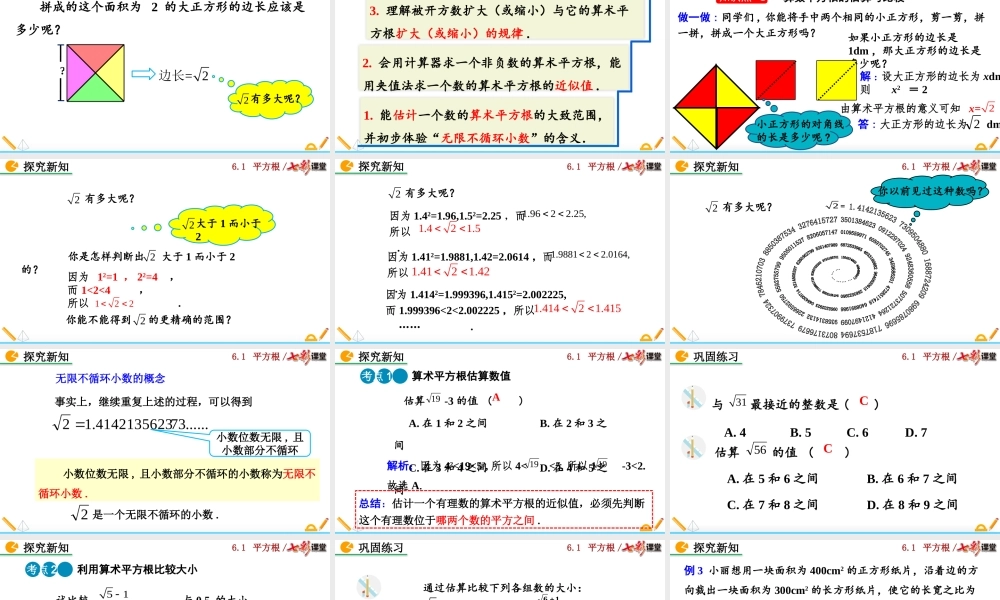
人教版数学七年级下册6.1平方根(第2课时)6.1平方根/拼成的这个面积为2的大正方形的边长应该是多少呢？?有多大呢？2=2边长导入新知6.1平方根/2.会用计算器求一个非负数的算术平方根，能用夹值法求一个数的算术平方根的近似值.1.能估计一个数的算术平方根的大致范围，并初步体验“无限不循环小数”的含义．学习目标3.理解被开方数扩大（或缩小）与它的算术平方根扩大（或缩小）的规律.6.1平方根/探究新知知识点1算数平方根的估算与比较做一做:同学们,你能将手中两个相同的小正方形，剪一剪，拼一拼，拼成一个大正方形吗？如果小正方形的边长是1dm，那大正方形的边长是多少呢？解:设大正方形的边长为xdm则答:大正方形的边长为dm2x2＝2小正方形的对角线的长是多少呢?由算术平方根的意义可知x=26.1平方根/有多大呢？2你是怎样判断出大于1而小于2的？2大于1而小于22因为12=1，22=4，而，所以．探究新知1<2<4122你能不能得到的更精确的范围？26.1平方根/有多大呢？21.9622.25,……探究新知因为1.42=1.96,1.52=2.25，而所以.1.421.5因为1.412=1.9881,1.42=2.0614，而所以.1.4121.421.988122.0164,因为1.4142=1.999396,1.4152=2.002225,而1.999396<2<2.002225，所以.1.41421.4156.1平方根/有多大呢？22你以前见过这种数吗？探究新知6.1平方根/小数位数无限,且小数部分不循环事实上，继续重复上述的过程，可以得到小数位数无限,且小数部分不循环的小数称为无限不循环小数.无限不循环小数的概念探究新知......734142135623.12是一个无限不循环的小数.26.1平方根/估算-3的值()A.在1和2之间B.在2和3之间C.在3和4之间D.在4和5之间19A总结：估计一个有理数的算术平方根的近似值，必须先判断这个有理数位于哪两个数的平方之间.探究新知算术平方根估算数值解析：因为42<19<52,所以4<<5,所以1<-3<2.故选A.1919考点16.1平方根/与最接近的整数是()A.4B.5C.6D.7C巩固练习估算的值()A.在5和6之间B.在6和7之间C.在7和8之间D.在8和9之间5631C6.1平方根/试比较与0.5的大小.512212215.0，25510.5.2，212215，222)5(探究新知利用算术平方根比较大小提示：比较数的大小，先估计其算术平方根的近似值.解:考点26.1平方根/通过估算比较下列各组数的大小：(1)与1.9；(2)与1.5.6125解：(1)因为5>4，所以>2，所以>1.9.55(2)因为6>4，所以>2，所以>=1.5.6612212巩固练习6.1平方根/例3小丽想用一块面积为400cm2的正方形纸...