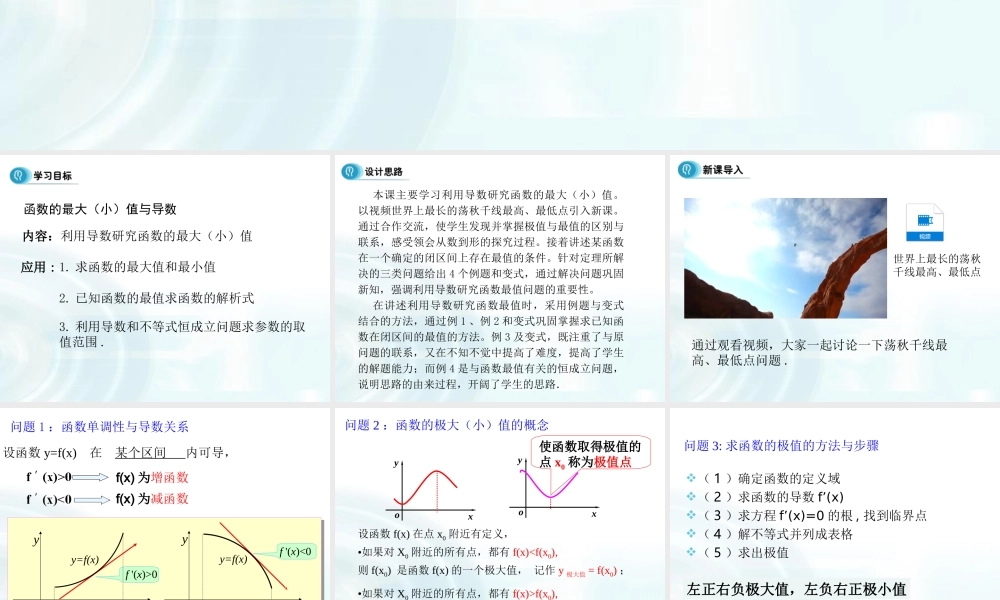
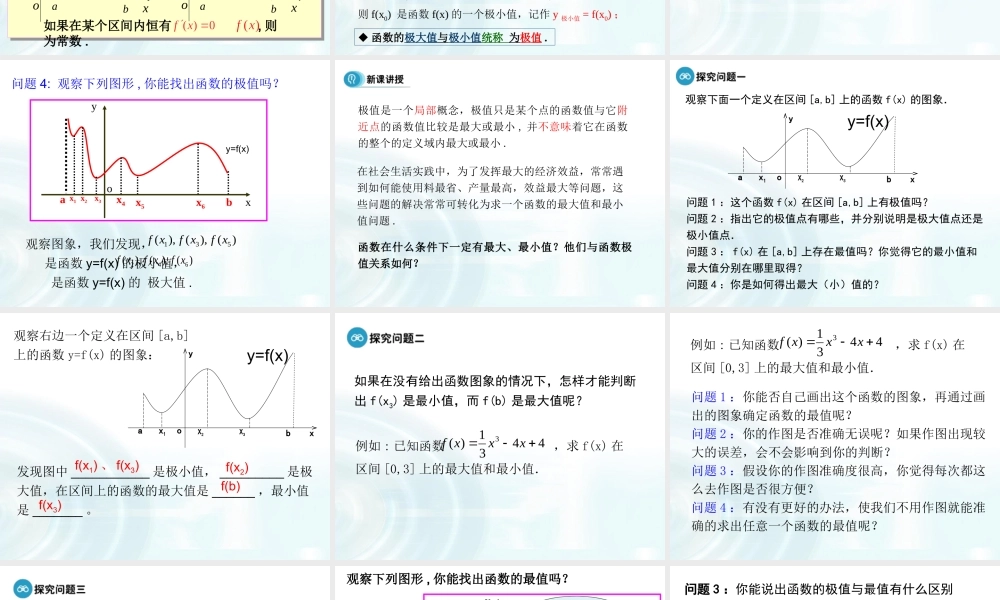
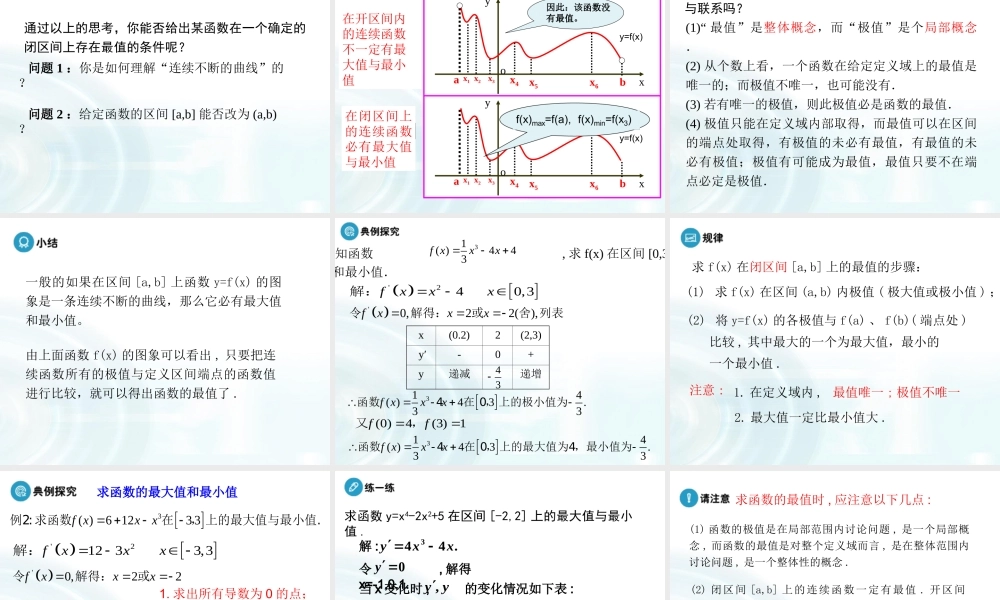
3.3.3函数的最大(小)值与导数函数的最大(小)值与导数内容:利用导数研究函数的最大(小)值应用:1.求函数的最大值和最小值2.已知函数的最值求函数的解析式3.利用导数和不等式恒成立问题求参数的取值范围.本课主要学习利用导数研究函数的最大(小)值。以视频世界上最长的荡秋千线最高、最低点引入新课。通过合作交流,使学生发现并掌握极值与最值的区别与联系,感受领会从数到形的探究过程。接着讲述某函数在一个确定的闭区间上存在最值的条件。针对定理所解决的三类问题给出4个例题和变式,通过解决问题巩固新知,强调利用导数研究函数最值问题的重要性。在讲述利用导数研究函数最值时,采用例题与变式结合的方法,通过例1、例2和变式巩固掌握求已知函数在闭区间的最值的方法。例3及变式,既注重了与原问题的联系,又在不知不觉中提高了难度,提高了学生的解题能力;而例4是与函数最值有关的恒成立问题,说明思路的由来过程,开阔了学生的思路.通过观看视频,大家一起讨论一下荡秋千线最高、最低点问题.世界上最长的荡秋千线最高、最低点aby=f(x)xoyy=f(x)xoyabf'(x)>0f'(x)<0问题1:函数单调性与导数关系如果在某个区间内恒有,则为常数.设函数y=f(x)在某个区间内可导,f(x)为增函数f(x)为减函数问题2:函数的极大(小)值的概念设函数f(x)在点x0附近有定义,•如果对X0附近的所有点,都有f(x)f(x0),则f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0);oxyoxy◆函数的极大值与极小值统称为极值.使函数取得极值的点x0称为极值点(1)确定函数的定义域(2)求函数的导数f’(x)(3)求方程f’(x)=0的根,找到临界点(4)解不等式并列成表格(5)求出极值问题3:求函数的极值的方法与步骤左正右负极大值,左负右正极小值xoyax1by=f(x)x2x3x4x5x6问题4:观察下列图形,你能找出函数的极值吗?135(),(),()fxfxfx观察图象,我们发现,是函数y=f(x)的极小值,是函数y=f(x)的极大值.246(),(),()fxfxfx在社会生活实践中,为了发挥最大的经济效益,常常遇到如何能使用料最省、产量最高,效益最大等问题,这些问题的解决常常可转化为求一个函数的最大值和最小值问题.函数在什么条件下一定有最大、最小值?他们与函数极值关系如何?极值是一个局部概念,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内...