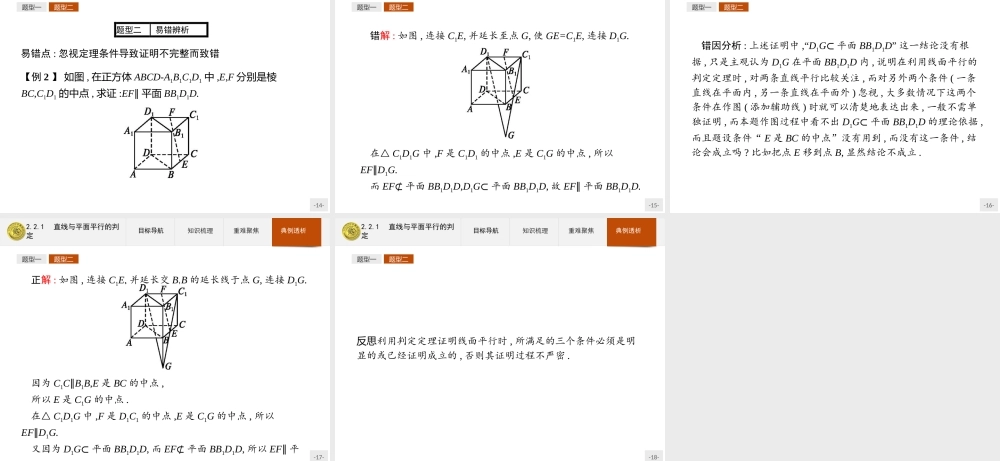
-1-2.2直线、平面平行的判定及其性质-2-2.2.1直线与平面平行的判定-3-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析1.理解并掌握直线与平面平行的判定定理,明确定理中“平面外”三个字的重要性.2.能利用判定定理证明线面平行问题.-4-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析直线与平面平行的判定定理文字语言平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行图形语言符号语言a⊄α,b⊂α,且a∥b⇒a∥α作用证明直线与平面平行-5-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析【做一做】如图,E,F分别为三棱锥A-BCD的棱BC,BA上的点,且BE∶BC=BF∶BA=1∶3.求证:EF∥平面ACD.证明:因为BE∶BC=BF∶BA=1∶3,所以EF∥AC.又EF⊄平面ACD,AC⊂平面ACD,所以EF∥平面ACD.-6-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析121.理解直线与平面平行的判定定理剖析:(1)此定理可以简记为:若线线平行,则线面平行.线线平行是条件,是平面问题,而线面平行是结论,是空间问题.这一定理体现了空间问题向平面问题转化的思想.(2)要证明平面外的一条直线和这个平面平行,只要在这个平面内找到一条直线和已知直线平行即可.(3)定理中的三个条件a∥b,a⊄α,b⊂α缺一不可.-7-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析12名师点拨在证明线面平行时,一定要说明一条直线在平面内,一条直线在平面外,这样才可以得到结论.-8-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析122.一条直线平行于一个平面内的无数条直线,这条直线不一定平行于这个平面剖析:可通过举反例,明确直线与平面平行的判定定理的使用条件.例如:如图,在长方体ABCD-A1B1C1D1中,在棱AB上任取一点E,过点E作EF∥AD交CD于点F,用同样的方法可以在平面AC内作出无数条与AD平行的直线,很明显直线AD平行于平面AC内的这无数条直线,但是AD⊂平面AC.所以一条直线平行于一个平面内的无数条直线,这条直线不一定平行于这个平面.故判定直线a和平面α平行时,必须具备三个条件.-9-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析题型一题型二题型一证明直线与平面平行【例1】如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥平面AA1B1B.-10-2.2.1直线与平面平行的判定目标导航知识梳理重难聚焦典例透析题型一题型二证明:如图,作ME∥BC,交BB1于点E,作NF∥AD,交AB于点F,连接EF,则EF⊂平面AA1B1B,...