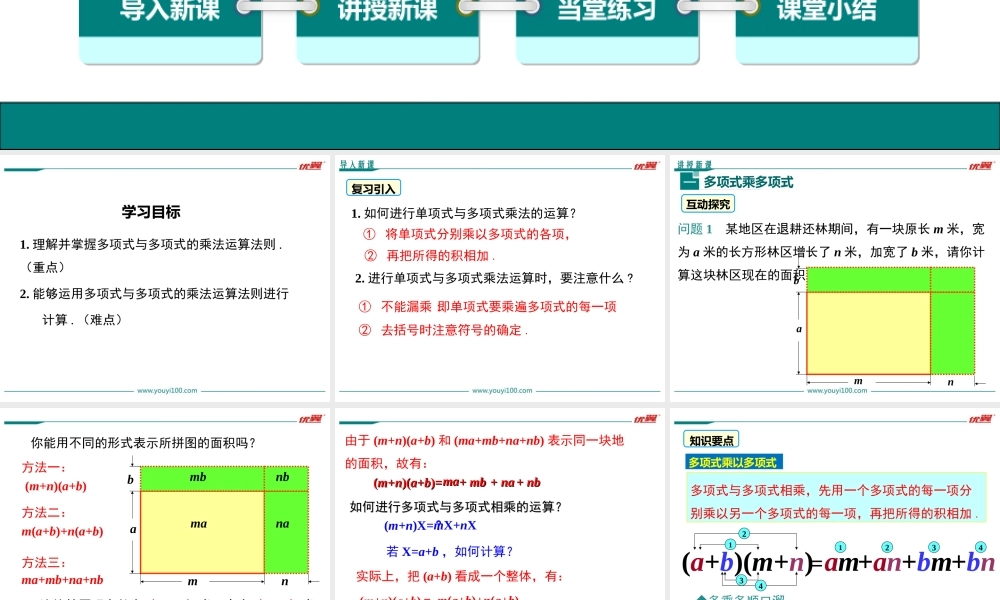
14.1.4整式乘法第十四章整式的乘法与因式分解优翼课件导入新课讲授新课当堂练习课堂小结第2课时多项式与多项式相乘八年级数学上(RJ)教学课件学习目标1.理解并掌握多项式与多项式的乘法运算法则.(重点)2.能够运用多项式与多项式的乘法运算法则进行计算.(难点)导入新课复习引入1.如何进行单项式与多项式乘法的运算?②再把所得的积相加.①将单项式分别乘以多项式的各项,2.进行单项式与多项式乘法运算时,要注意什么?①不能漏乘:即单项式要乘遍多项式的每一项②去括号时注意符号的确定.讲授新课多项式乘多项式一互动探究问题1某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区增长了n米,加宽了b米,请你计算这块林区现在的面积.ambnmanambnbambn你能用不同的形式表示所拼图的面积吗?这块林区现在长为(m+n)米,宽为(a+b)米(m+n)(a+b)m(a+b)+n(a+b)ma+mb+na+nb方法一:方法二:方法三:由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:((mm++nn)()(aa++bb)=)=mama++mbmb++nana++nbnb如何进行多项式与多项式相乘的运算?如何进行多项式与多项式相乘的运算?实际上,把(a+b)看成一个整体,有:=ma+mb+na+nb(m+n)(a+b)=m(a+b)+n(a+b)(m+n)X=mX+nX?若X=a+b,如何计算?多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.知识要点多项式乘以多项式1234(a+b)(m+n)=am1234+an+bm+bn多乘多顺口溜:多乘多,来计算,多项式各项都见面,乘后结果要相加,化简、排列才算完.典例精析例1计算:(1)(3x+1)(x+2);(2)(x-8y)(x-y);(3)(x+y)(x2-xy+y2).解:(1)原式=3x·x+2·3x+1·x+1×2=3x2+6x+x+2(2)原式=x·x-xy-8xy+8y2结果中有同类项的要合并同类项.=3x2+7x+2;计算时要注意符号问题.=x2-9xy+8y2;(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2=x3-x2y+xy2+x2y-xy2+y3=x3+y3.需要注意的几个问题需要注意的几个问题:(1):(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式.注意计算时不能漏乘.例2先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.当a=-1,b=1时,解:原式=a3-8b3-(a2-5ab)(a+3b)=a3-8b3-a3-3a2b+5a2b+15ab2=-8b3+2a2b+15ab2.原式=-8+2-15=-21.例3已知ax2+bx+1(a≠0)与3x-2的积不含x2项,也不含x项,求系数a、b的值.解:(ax2+bx+1)(3x-2)=3ax3-2ax2+3bx2-2bx+3x-2, 积不含x2的项,也不含x的项,230,230,abb...