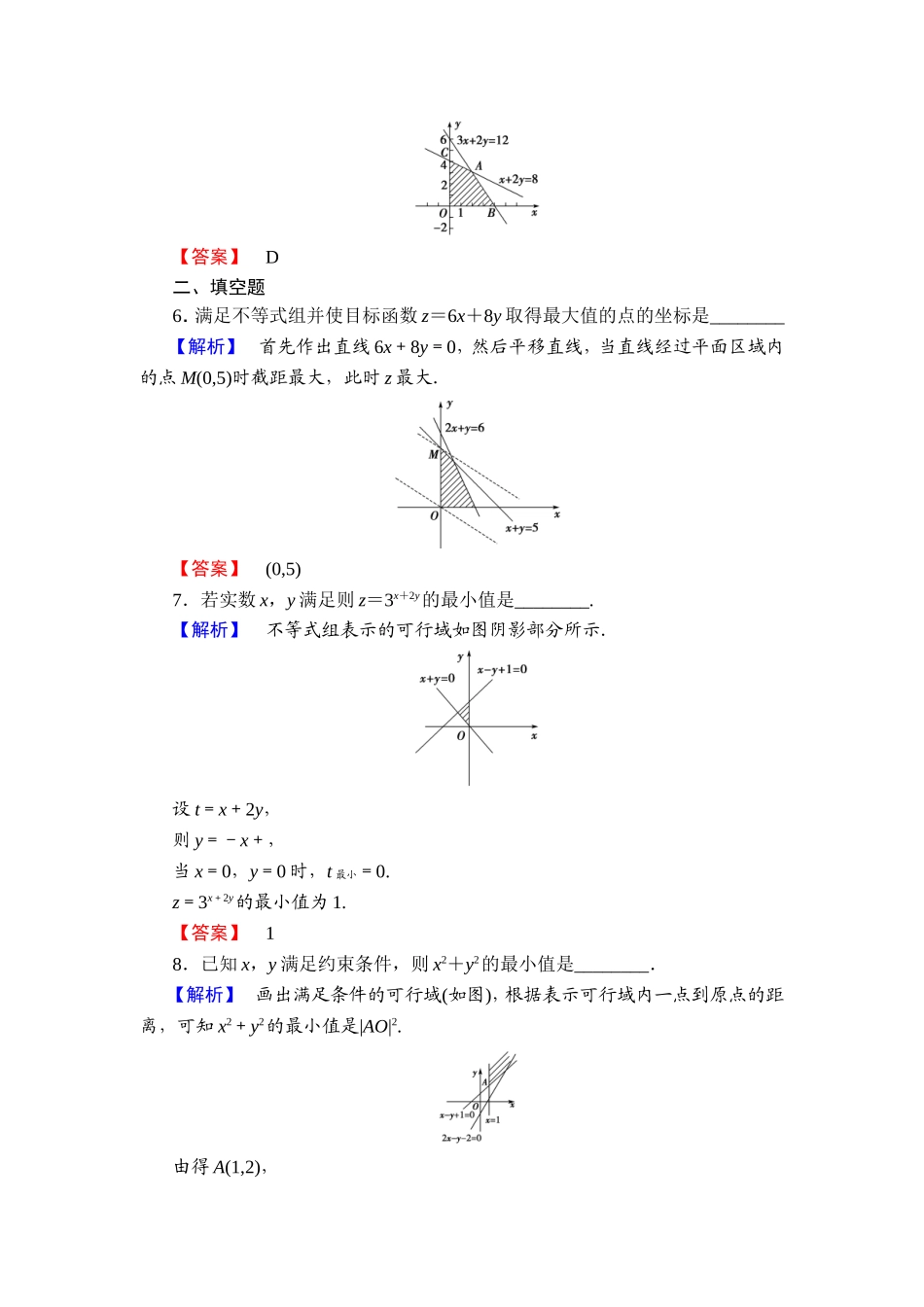
学业分层测评(二十)(建议用时:45分钟)[学业达标]一、选择题1.某服装制造商有10m2的棉布料,10m2的羊毛料和6m2的丝绸料,做一条裤子需要1m2的棉布料,2m2的羊毛料和1m2的丝绸料,做一条裙子需要1m2的棉布料,1m2的羊毛料和1m2的丝绸料,做一条裤子的纯收益是20元,一条裙子的纯收益是40元,为了使收益达到最大,若生产裤子x条,裙子y条,利润为z,则生产这两种服装所满足的数学关系式与目标函数分别为()A.z=20x+40yB.z=20x+40yC.z=20x+40yD.z=40x+20y【解析】由题意易知选A.【答案】A2.若变量x,y满足约束条件则z=2x-y的最小值等于()A.-B.-2C.-D.2【解析】作出可行域如图,由图可知,当直线z=2x-y过点A时,z值最小.由得点A,zmin=2×(-1)-=-.【答案】A3.设变量x,y满足约束条件则目标函数z=3x-y的取值范围是()A.B.C.D.【解析】作出可行域如图所示.目标函数z=3x-y可转化为y=3x-z,作l0:3x-y=0,在可行域内平移l0,可知在A点处z取最小值为-,在B点处z取最大值为6.【答案】A4.已知实数x,y满足条件若目标函数z=mx-y(m≠0)取得最大值时的最优解有无穷多个,则实数m的值为()A.1B.C.-D.-1【解析】作出不等式组表示的平面区域如图阴影部分(包含边界)所示,由图可知当直线y=mx-z(m≠0)与直线2x-2y+1=0重合,即m=1时,目标函数z=mx-y取最大值的最优解有无穷多个,故选A.【答案】A5.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为()甲乙原料限额A(吨)3212B(吨)128A.12万元B.16万元C.17万元D.18万元【解析】设每天生产甲、乙产品分别为x吨、y吨,每天所获利润为z万元,则有z=3x+4y,作出可行域如图阴影部分所示,由图形可知,当直线z=3x+4y经过点A(2,3)时,z取最大值,最大值为3×2+4×3=18.【答案】D二、填空题6.满足不等式组并使目标函数z=6x+8y取得最大值的点的坐标是________【解析】首先作出直线6x+8y=0,然后平移直线,当直线经过平面区域内的点M(0,5)时截距最大,此时z最大.【答案】(0,5)7.若实数x,y满足则z=3x+2y的最小值是________.【解析】不等式组表示的可行域如图阴影部分所示.设t=x+2y,则y=-x+,当x=0,y=0时,t最小=0.z=3x+2y的最小值为1.【答案】18.已知x,y满足约束条件,则x2+y2的最小值是________.【...