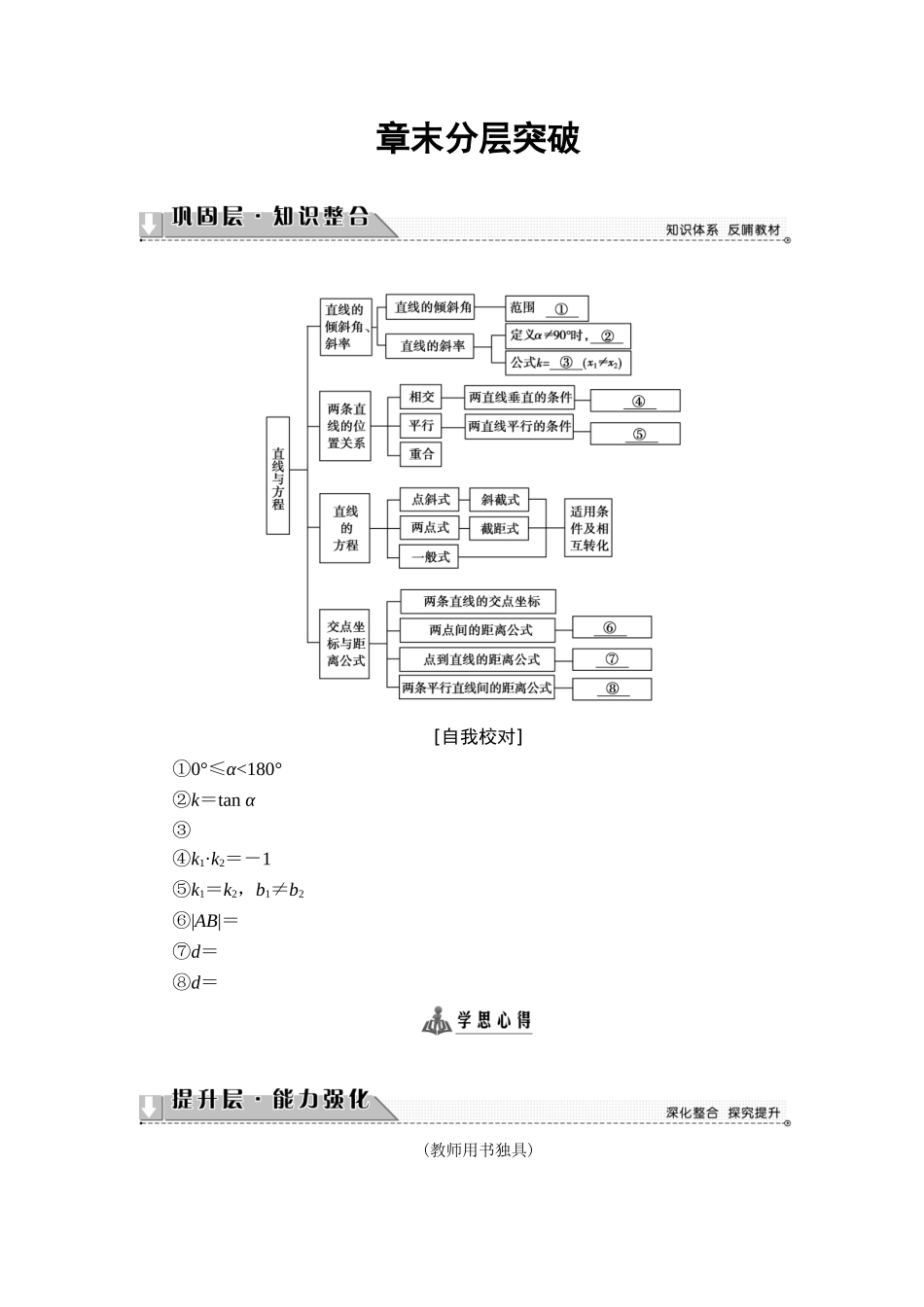
章末分层突破[自我校对]①0°≤α<180°②k=tanα③④k1·k2=-1⑤k1=k2,b1≠b2⑥|AB|=⑦d=⑧d=(教师用书独具)直线方程及其应用(1)求直线方程的主要方法是待定系数法,要掌握直线方程五种形式的适用条件及相互转化,能根据条件灵活选用方程,当不能确定某种方程条件具备时要另行讨论条件不满足的情况.(2)运用直线系方程的主要作用在于能使计算简单.过点A(-5,-4)作一直线l,使它与两坐标轴相交且与两轴所围成的三角形的面积为5,求直线l的方程.【精彩点拨】已知直线过定点A,且与两坐标轴都相交,围成的直角三角形的面积已知.求直线方程时可采用待定系数法,设出直线方程的点斜式,再由面积为5列方程,求直线的斜率.【规范解答】由题意知,直线l的斜率存在.设直线为y+4=k(x+5),交x轴于点,交y轴于点(0,5k-4),S=××|5k-4|=5,得25k2-30k+16=0(无实根),或25k2-50k+16=0,解得k=,或k=,所以所求直线l的方程为2x-5y-10=0,或8x-5y+20=0.[再练一题]1.过点P(-1,0),Q(0,2)分别作两条互相平行的直线,使它们在x轴上截距之差的绝对值为1,求这两条直线的方程.【解】(1)当两条直线的斜率不存在时,两条直线的方程分别为x=-1,x=0,它们在x轴上截距之差的绝对值为1,满足题意;(2)当直线的斜率存在时,设其斜率为k,则两条直线的方程分别为y=k(x+1),y=kx+2.令y=0,分别得x=-1,x=-.由题意得=1,即k=1.则直线的方程为y=x+1,y=x+2,即x-y+1=0,x-y+2=0.综上可知,所求的直线方程为x=-1,x=0,或x-y+1=0,x-y+2=0.直线的位置关系利用直线的方程判定两条直线的平行或垂直关系是这部分知识常涉及的题型.求解时,可以利用斜率之间的关系判定;若方程都是一般式,知道平行或垂直关系,求参数的值时也可用如下方法:直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.(1)l1∥l2时,可令A1B2-A2B1=0,解得参数的值后,再代入方程验证,排除重合的情况;(2)l1⊥l2时,可利用A1A2+B1B2=0直接求参数的值.已知直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,求m的值,使得(1)l1⊥l2;(2)l1∥l2.【精彩点拨】已知两直线的方程中都含有参数,求不同的位置关系时参数的取值,可以利用平行(或垂直)的条件列方程求解.【规范解答】法一当m=0或2时,两直线既不平行,也不垂直;当m≠0且m≠2时,直线l1,l2的斜率分别为:-,.(1)若l1⊥l2,则-·=-1,解得m=.(2)若l1∥l2,则由-=,得m...