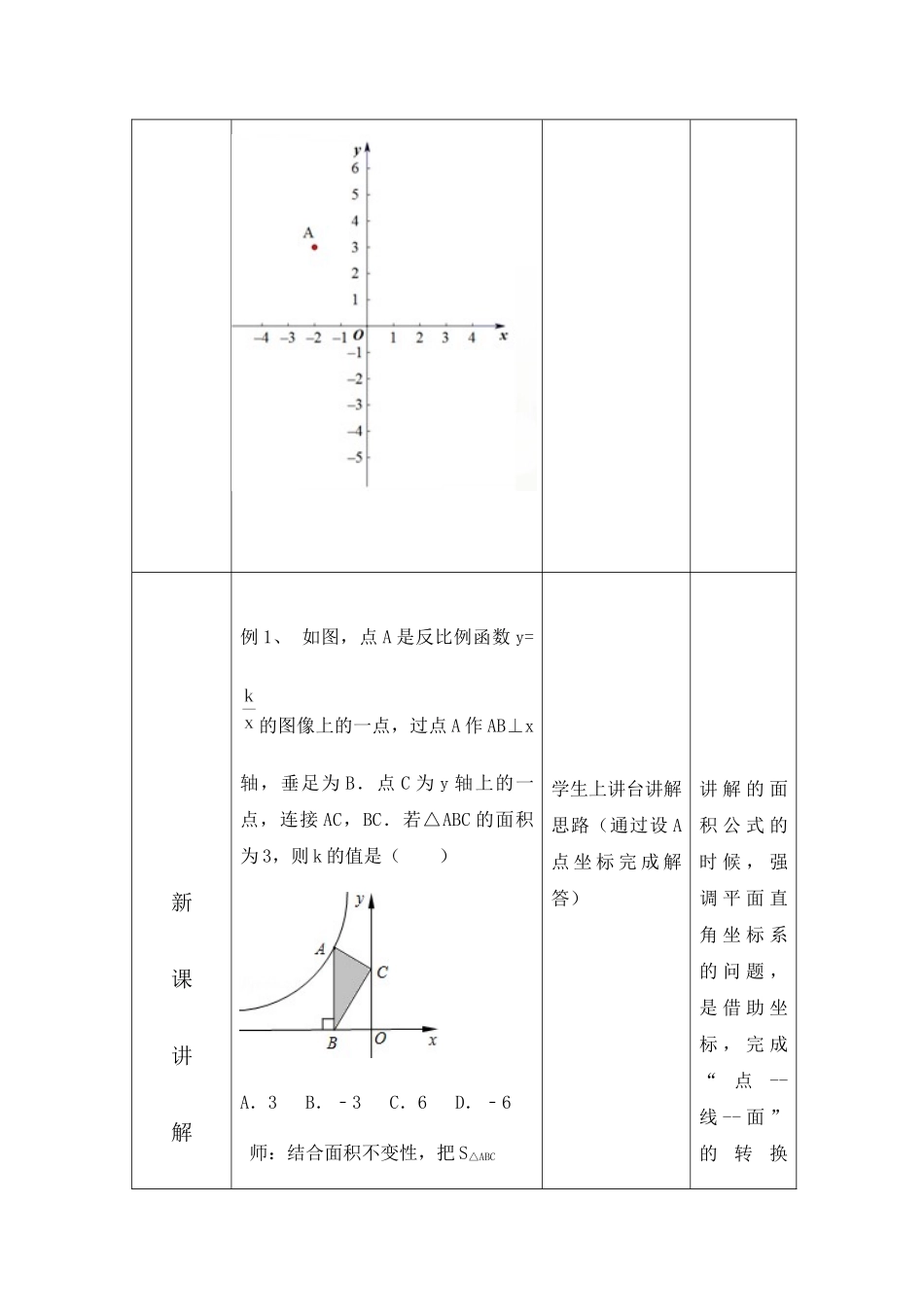
《反比例函数复习》教学设计一、教学目标(一)知识技能1.了解反比例函数的意义;2.掌握反比例函数的图像、性质,能利用图像、性质解题;3.掌握用待定系数法求反比例函数解析式;4.能灵活运用反比例函数的性质解决问题.(二)情感、态度通过思考、探索来激发学生学习的积极主动性,使学生获得一些研究问题的经验和方法;借助学生的讲解让学生真正成为课堂的主人,发展实践能力与积极进取的精神.二、教学重点、难点掌握利用待定系数法求反比例函数解析式,能灵活运用反比例函数的性质解决问题.三、教学方法引导、发现、创新、总结.四、教学过程教学环节教师活动学生活动点评知识梳已知,反比例函数经过点A(-2,3)(1)反比例函数的解析式为;师:这是反比例函数的定义,当k<0,图像位于二、四象限;学生完成课前预习内容,结合反比例函数的定义巧设基础问题,引入各个知理(2)若点P在此反比例函数上,PH⊥x轴于点H,则S△OPH=;师:体现了面积不变性;(3)过OA的直线与双曲线另一个交点为点B,则点B的坐标为;师:复习了反比例函数的对称性;(4)设反比例函数的解析式为,直线OA的解析式为,若,则x的范围是;(5)若x≥2,则y的取值范围是.师:体现了反比例函数的增减性。性质,对知识进行梳理。学生上黑板进行标注识点的分析,引导学生的思维进入学习新知的“佳境”。培养学生体会“想——做——想”的数学活动过程。新课讲解例1、如图,点A是反比例函数y=的图像上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是()A.3B.﹣3C.6D.﹣6师:结合面积不变性,把S△ABC学生上讲台讲解思路(通过设A点坐标完成解答)讲解的面积公式的时候,强调平面直角坐标系的问题,是借助坐标,完成“点--线--面”的转换转化为S△ABO,并启发学生借助三角形面积=,来解决问题。师:及时总结,反比例函数中的三角形面积问题,往往可以借助面积不变性或者坐标来解决问题。例2、如图,已知双曲线y=﹣(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为()A.6B.C.3D.2变式训练学生上讲台讲解思路,1、通过设坐标求解三角形的面积2、利用面积不变性求解面积。的。让学生动手操作、自主探索、合作交流。发展学生的动手操作、自主探究、合作交流和推理能力,提高学生分析问题和解决问题的能力。实践应用如图,点A是反比例函数在第二象限内图像上一点,点B是反比例函数在第一象限内图...