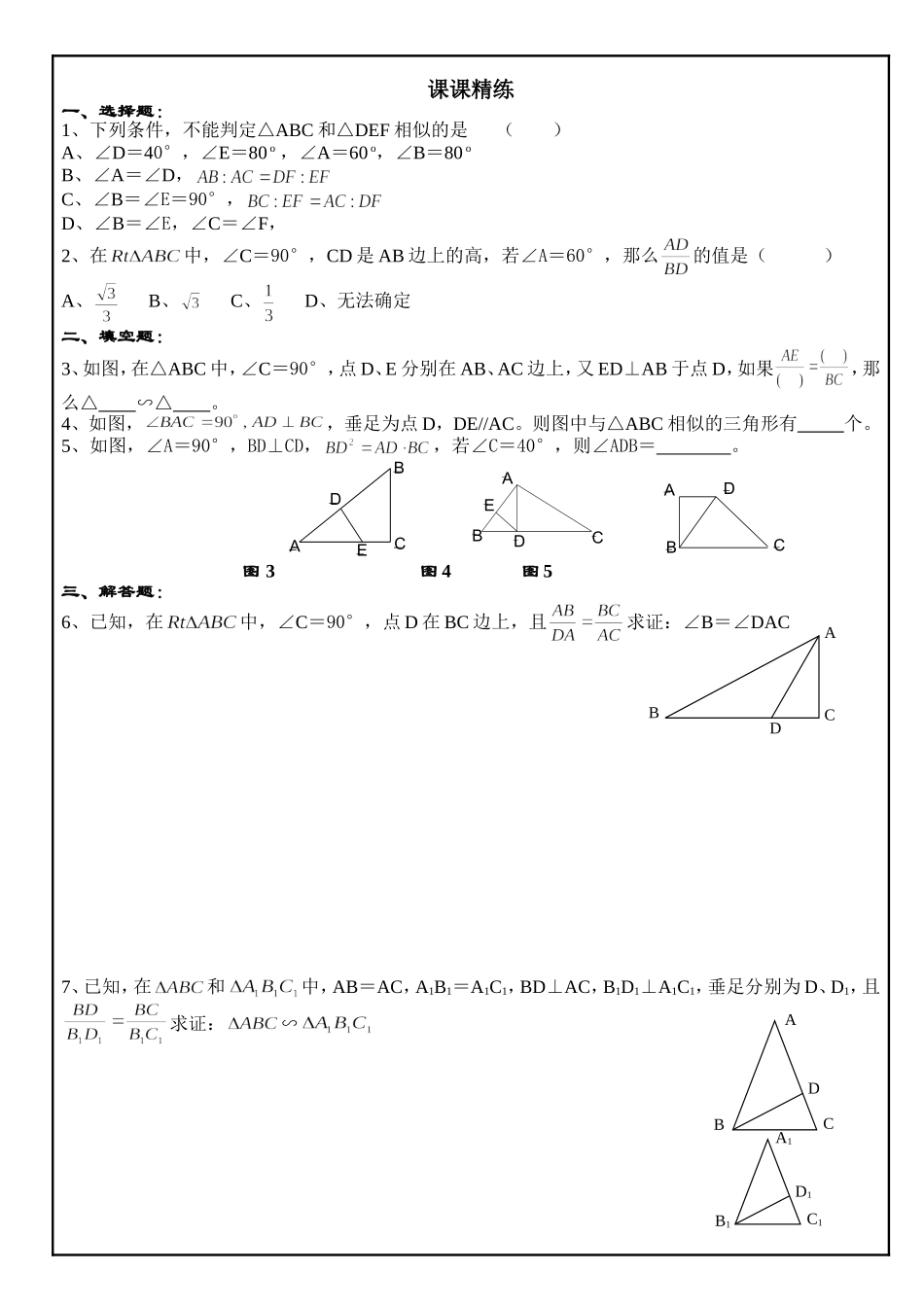
学生编号学生姓名授课教师辅导学科数学所属年级九年级教材版本沪教版课题名称相似三角形的判定4课时进度授课时间月日教学目标如下重点难点如下§24.4相似三角形的判定(4)学习目标1、类比直角三角形全等(HL)的判定探索直角三角形相似的特殊判定定理4;2、掌握并运用这一判定定理解决有关问题;3、进一步巩固三角形相似的判定定理1、2、3。学习重点熟练直角三角形判定定理4。学习难点了解判定定理4的证题方法与思路,并能灵活应用定理。学习过程一、学前准备1、我们已学过的判定三角形相似的定理有:。2、在RtΔABC与RtΔDEF中,∠C=∠F=90°,依据下列各组条件判定这两个三角形是否相似,并说明理由。1)∠A=55°∠D=35°;2)AC=9,BC=12,DF=6,EF=8;3)AC=3,BC=4,DF=6,DE=8;4)AB=10,AC=6,DE=15,EF=9;二、探究活动1、如图,在和中,如果且,那么和相似吗?思路点拨:抓住已学判定方法,着手研究证明方法。2、判定定理4:斜边和直角边对应成比例,两个直角三角形相似。CBAC1B1A1符号语言:3、如图,在四边形ABCD中,,AD=a,BC=b,,求证:DC⊥BC4、已知:如图,在和中,,,,垂足分别为D、D1,且求证:∽三、自我测验1、如图,在中,于D,下列条件:1)2)3)4),其中一定能判定是直角三角形的共有()A、3个B、2个C、1个D、0个2、在中,,求证:EDCBA_D_C_B_AABCDA1B1C1D1ABCD课课精练一、选择题:1、下列条件,不能判定△ABC和△DEF相似的是()A、∠D=40°,∠E=80o,∠A=60o,∠B=80oB、∠A=∠D,C、∠B=∠E=90°,D、∠B=∠E,∠C=∠F,2、在中,∠C=90°,CD是AB边上的高,若∠A=60°,那么的值是()A、B、C、D、无法确定二、填空题:3、如图,在△ABC中,∠C=90°,点D、E分别在AB、AC边上,又ED⊥AB于点D,如果,那么△∽△。4、如图,,垂足为点D,DE//AC。则图中与△ABC相似的三角形有个。5、如图,∠A=90°,BD⊥CD,,若∠C=40°,则∠ADB=。图3图4图5三、解答题:6、已知,在中,∠C=90°,点D在BC边上,且求证:∠B=∠DAC7、已知,在和中,AB=AC,A1B1=A1C1,BD⊥AC,B1D1⊥A1C1,垂足分别为D、D1,且求证:∽_E_D_A_B_C_E_D_C_B_A_D_C_B_AACBDABCDA1D1C1B18、如图,梯形ABCD中,AD∥BC,∠A=90°,AD=2,BC=3,AB=7,点P是边AB上的一点,当P在何处时,△APD与△BPC相似?四、课外拓展:1、已知,在中,,E是BC的中点,DE交AC的延长线于点F。求证:2、如图,当BD与a、b满足怎样的关系式时,这两个三角形相似?ADBPCFEDCBA