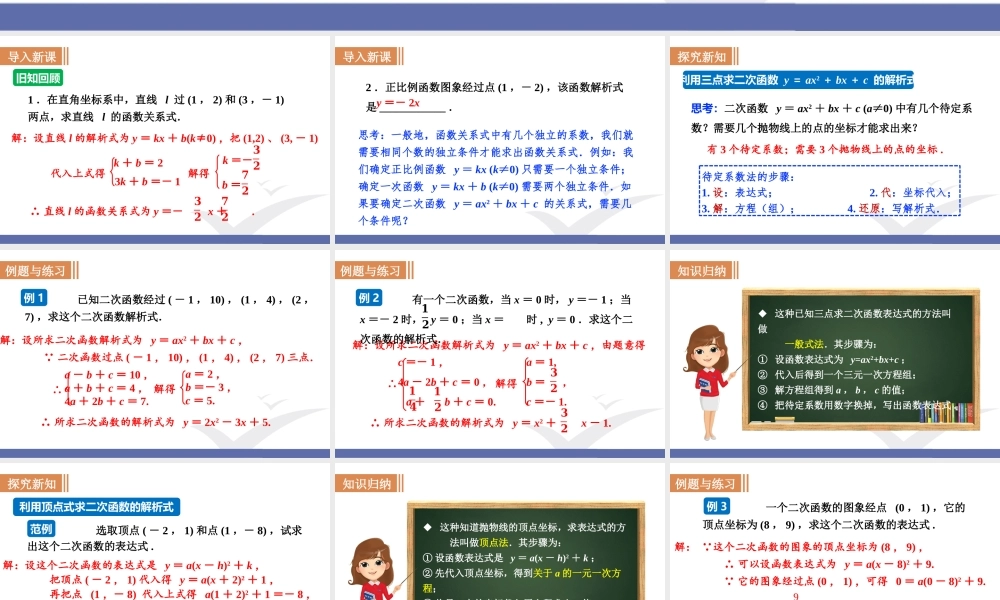
第二十一章二次函数与反比例函数21.2二次函数的图象和性质第6课时二次函数表达式的确定导入新课旧知回顾1.在直角坐标系中,直线l过(1,2)和(3,-1)两点,求直线l的函数关系式.解:设直线l的解析式为y=kx+b(k≠0),把(1,2)、(3,-1)k+b=23k+b=-1代入上式得k=-𝟑𝟐b=𝟕𝟐解得∴直线l的函数关系式为y=-x+.𝟑𝟐𝟕𝟐导入新课2.正比例函数图象经过点(1,-2),该函数解析式是____________.y=-2x思考:一般地,函数关系式中有几个独立的系数,我们就需要相同个数的独立条件才能求出函数关系式.例如:我们确定正比例函数y=kx(k≠0)只需要一个独立条件;确定一次函数y=kx+b(k≠0)需要两个独立条件.如果要确定二次函数y=ax2+bx+c的关系式,需要几个条件呢?探究新知利用三点求二次函数y=ax2+bx+c的解析式思考:二次函数y=ax2+bx+c(a≠0)中有几个待定系数?需要几个抛物线上的点的坐标才能求出来?有3个待定系数;需要3个抛物线上的点的坐标.待定系数法的步骤:1.设:表达式;2.代:坐标代入;3.解:方程(组);4.还原:写解析式.例题与练习已知二次函数经过(-1,10),(1,4),(2,7),求这个二次函数解析式.例1解:设所求二次函数解析式为y=ax2+bx+c, 二次函数过点(-1,10),(1,4),(2,7)三点.∴所求二次函数的解析式为y=2x2-3x+5.∴a-b+c=10,a+b+c=4,4a+2b+c=7.a=2,b=-3,c=5.解得例题与练习解:设所求二次函数解析式为y=ax2+bx+c,由题意得有一个二次函数,当x=0时,y=-1;当x=-2时,y=0;当x=时,y=0.求这个二次函数的解析式.𝟏𝟐∴所求二次函数的解析式为y=x2+x-1.𝟑𝟐∴c=-1,4a-2b+c=0,a+b+c=0.𝟏𝟒𝟏𝟐例2a=1,b=,c=-1.𝟑𝟐解得知识归纳◆这种已知三点求二次函数表达式的方法叫做一般式法.其步骤为:①设函数表达式为y=ax2+bx+c;②代入后得到一个三元一次方程组;③解方程组得到a,b,c的值;④把待定系数用数字换掉,写出函数表达式.探究新知利用顶点式求二次函数的解析式选取顶点(-2,1)和点(1,-8),试求出这个二次函数的表达式.解:设这个二次函数的表达式是y=a(x-h)2+k,把顶点(-2,1)代入得y=a(x+2)2+1,再把点(1,-8)代入上式得a(1+2)2+1=-8,解得a=-1.∴所求的二次函数的表达式是y=-(x+2)2+1或y=-x2-4x-3.范例知识归纳◆这种知道抛物线的顶点坐标,求表达式的方法叫做顶点法.其步骤为:①设函数表达式是y=a(x-h...