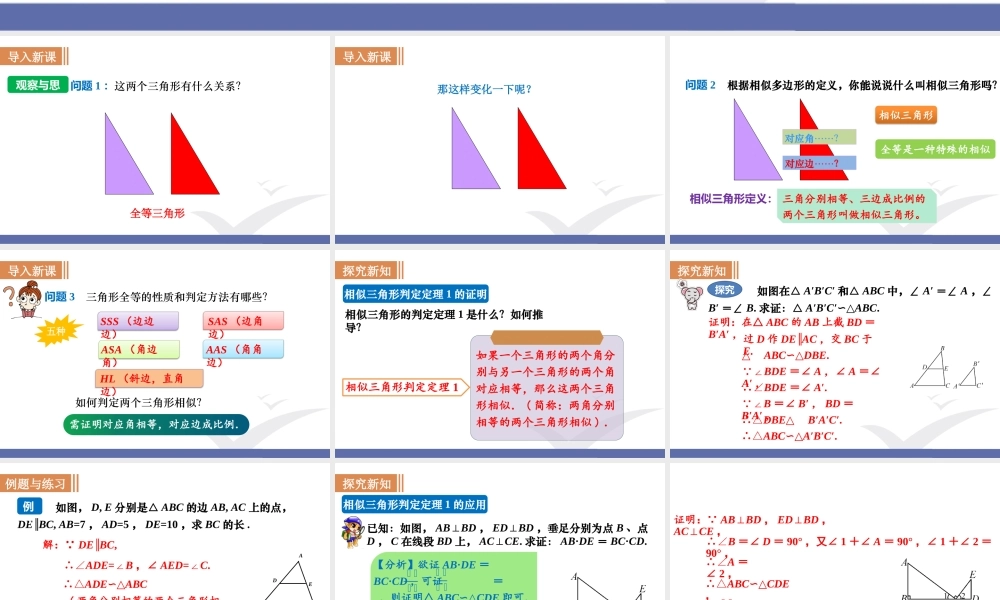
第二十二章相似形第2课时相似三角形的判定(2)22.2相似三角形的判定导入新课观察与思考问题1:这两个三角形有什么关系?全等三角形导入新课那这样变化一下呢?相似三角形定义:对应角……?对应边……?问题2根据相似多边形的定义,你能说说什么叫相似三角形吗?相似三角形全等是一种特殊的相似三角分别相等、三边成比例的两个三角形叫做相似三角形。导入新课SSS(边边边)如何判定两个三角形相似?问题3三角形全等的性质和判定方法有哪些?五种SAS(边角边)ASA(角边角)AAS(角角边)HL(斜边,直角边)需证明对应角相等,对应边成比例.探究新知相似三角形的判定定理1是什么?如何推导?相似三角形判定定理1相似三角形判定定理1的证明如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.(简称:两角分别相等的两个三角形相似).探究新知如图在△A′B′C′和△ABC中,∠A′=∠A,∠B′=∠B.求证:△A′B′C′∽△ABC.证明:在△ABC的AB上截BD=B′A′,探究过D作DE∥AC,交BC于E.△ABCDBE∽△.∴∠BDE=∠A′. ∠BDE=∠A,∠A=∠A′, ∠B=∠B′,BD=B′A′,∴△DBE△B′A′C′.∴△ABC∽△A′B′C′.例题与练习如图,D,E分别是△ABC的边AB,AC上的点,DEBC∥,AB=7,AD=5,DE=10,求BC的长.解: DEBC∥,BADEC例1∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC(两角分别相等的两个三角形相似).∴BC=14.∴=ࡰࡰࡰࡰࡰࡰࡰࡰ探究新知相似三角形判定定理1的应用已知:如图,AB⊥BD,ED⊥BD,垂足分别为点B、点D,C在线段BD上,AC⊥CE.求证:AB·DE=BC·CD.【分析】欲证AB·DE=BC·CD,可证=,则证明△ABC∽△CDE即可,由题意可知∠1+∠2=90°,∠1+∠A=90°,则∠2=∠A.于是Rt△ABC∽Rt△CDE.ࡰࡰࡰࡰࡰࡰࡰࡰ证明: AB⊥BD,ED⊥BD,AC⊥CE,∴∠B=∠D=90°,又∠1+∠A=90°,∠1+∠2=90°,∴∠A=∠2,∴△ABC∽△CDE,∴=,即AB·DE=BC·CD.ࡰࡰࡰࡰࡰࡰࡰࡰ例题与练习如图所示,在四边形ABCD中,AC平分∠DAB,∠ACD=∠ABC,求证:AC2=AB·AD.证明: AC平分∠DAB,例2又 ∠ACD=∠ABC,∴∠DAC=∠CAB,∴△ADC∽△ACB,∴AC2=AB·AD.∴=,ࡰࡰࡰࡰࡰࡰࡰࡰ随堂练习2.如图,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,当∠APD=60°时,CD的长为__________.61.如图,在△ABC中,∠ACB=90°,DE⊥AB于点E,BD=10,AC=BC,DE=___.ࡰࡰࡰࡰ3.如图:点G在平行四...