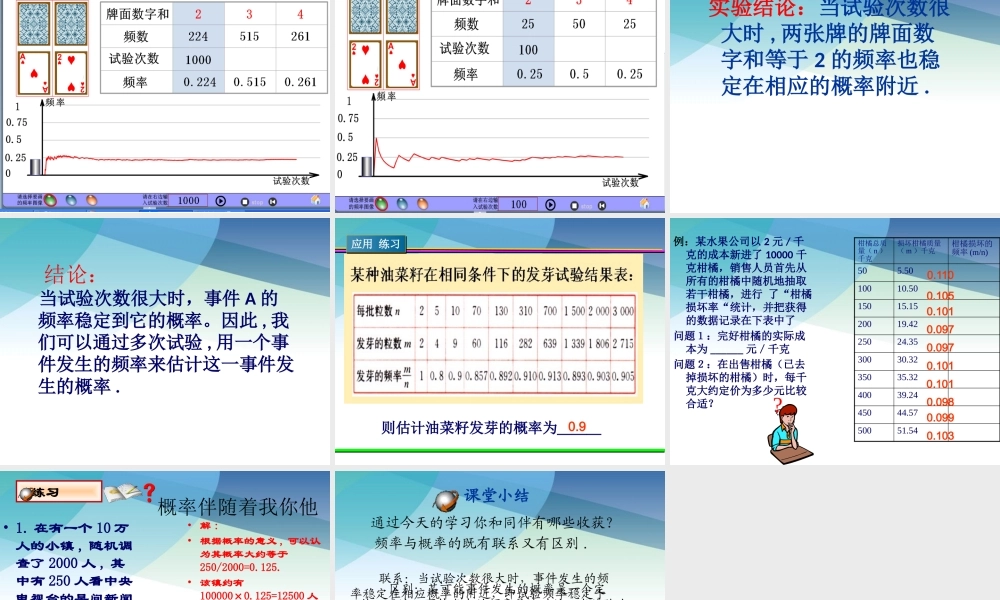
31.3用频率估计概率概率:一个数P(A)表示随机事件A发生的可能性大小,称P(A)为事件A的概率.P(A)=事件A包含的可能结果数/所有可能结果总数回顾与思考频率:每个考察对象出现的次数与总次数的比值称为频率.回顾练习还记得上节课做过的掷硬币试验吗?对掷硬币实验,当投掷次数很少时,频率很_____;当投掷次数很多时,正面向上的频率逐渐稳定到____,即____稳定到____.不稳定0.5频率概率回顾回顾则估计抛掷一枚硬币正面朝上的概率为__o.5摸牌实验探索频率与概率的关系两人为一个小组,每个小组两张相同的牌,牌面的数字分别是1和2,放入盒中.先从中任意取出一张记下数字,放回盒中,然后再取出一张记下数字,观察两个数字的和.(1)一次试验中两张牌的牌面的数字和可能有哪些值?2,3,4(2)每个结果发生的可能性相同吗?根据右表填空12123234P(和为2)=____P(和为3)=____P(和为4)=____1/41/21/4第一次第二次探究的方法•收集不同次数实验的频率数据•填写频率统计表整理数据•绘制频率的折线统计图•分析频率随着实验次数增加的变化趋势做一做每组做10次试验,依次记录每次摸得的牌面数字,并根据试验结果填写下表:牌面数字和234频数将全班各组的数据累计起来,相应得到试验20次、40次、60次、80次、100次、120次、140次、160次、180次,200次时两张牌的牌面数字和等于2与等于3发生的次数,计算相应的频率,并绘制相应的折线统计图。想一想说一说(1)在上面的试验中,你发现了什么?如果继续增加试验次数呢?(2)当实验次数很大时,你估计两张牌的牌面数字和等于3的频率大约是多少?你是怎样估计的?议一议想一想类比掷硬币的试验结论,你能估计出上述摸牌试验中两张牌的牌面数字和等于3的概率是多少吗?两张牌的牌面数字和等于3的理论概率为21动动脑筋(1)在上面的试验中,你发现了什么?如果继续增加试验次数呢?(2)当次数很大时,你估计两张牌的牌面数字和等于3的频率大约是多少?你试验是怎样估计的?议一议探究成果结论:当试验次数很大时,两张牌的牌面数字和等于3的频率也稳定在相应的概率附近.实验结论:当试验次数很大时,两张牌的牌面数字和等于2的频率也稳定在相应的概率附近.结论:当试验次数很大时,事件A的频率稳定到它的概率。因此,我们可以通过多次试验,用一个事件发生的频率来估计这一事件发生的概率.应用练习应用练习则估计油菜籽发芽的概率为___0.9例:某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘...