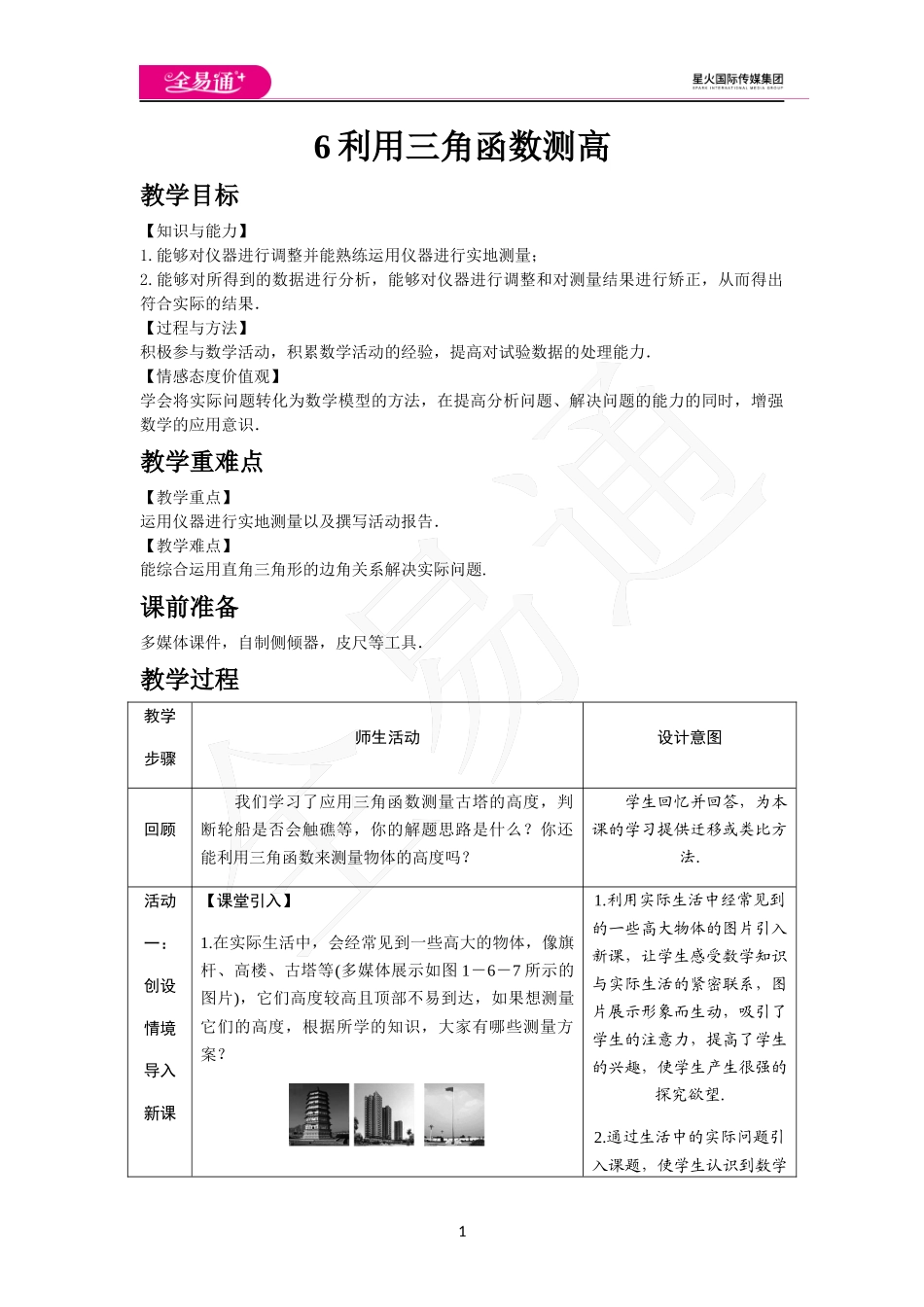
16利用三角函数测高教学目标【知识与能力】1.能够对仪器进行调整并能熟练运用仪器进行实地测量;2.能够对所得到的数据进行分析,能够对仪器进行调整和对测量结果进行矫正,从而得出符合实际的结果.【过程与方法】积极参与数学活动,积累数学活动的经验,提高对试验数据的处理能力.【情感态度价值观】学会将实际问题转化为数学模型的方法,在提高分析问题、解决问题的能力的同时,增强数学的应用意识.教学重难点【教学重点】运用仪器进行实地测量以及撰写活动报告.【教学难点】能综合运用直角三角形的边角关系解决实际问题.课前准备多媒体课件,自制侧倾器,皮尺等工具.教学过程教学步骤师生活动设计意图回顾我们学习了应用三角函数测量古塔的高度,判断轮船是否会触礁等,你的解题思路是什么?你还能利用三角函数来测量物体的高度吗?学生回忆并回答,为本课的学习提供迁移或类比方法.活动一:创设情境导入新课【课堂引入】1.在实际生活中,会经常见到一些高大的物体,像旗杆、高楼、古塔等(多媒体展示如图1-6-7所示的图片),它们高度较高且顶部不易到达,如果想测量它们的高度,根据所学的知识,大家有哪些测量方案?1.利用实际生活中经常见到的一些高大物体的图片引入新课,让学生感受数学知识与实际生活的紧密联系,图片展示形象而生动,吸引了学生的注意力,提高了学生的兴趣,使学生产生很强的探究欲望.2.通过生活中的实际问题引入课题,使学生认识到数学2图1-6-7(1)利用太阳光下的影子测量;(2)利用标杆测量;(3)利用镜子的反射测量.师:我们前面刚学过直角三角形的边角关系,那么能不能用这方面的知识来测量一些物体的高度呢?带着这个问题,我们来进行本节课的学习.2.如图1-6-8,AC表示一幢楼,它的各楼层都可到达;BD表示一个建筑物,且不能到达.已知AC与BD地平高度相同,AC周围没有开阔地带,仅有的测量工具为皮尺(可测量长度)和测角器(可测量仰角、俯角和两视线间的夹角).图1-6-8(1)请你设计一个测量建筑物BD高度的方案,要求写出测量步骤和必要的测量数据(用字母表示),并画出测量示意图;(2)写出计算BD高度的表达式.师:如何设计一个测量建筑物BD高度的方案呢?来源于生活,又服务于生活,增加学生学习数学的兴趣,并让学生带着问题走进今天的学习.活动二:实践探究交流新知【探究1】测量倾斜角(仰角或俯角)师:(课件展示)测量倾斜角可以用测倾器,简单的测倾器由度盘、铅锤和支杆组成(如图1-6-9).图1-6-9使学生会...