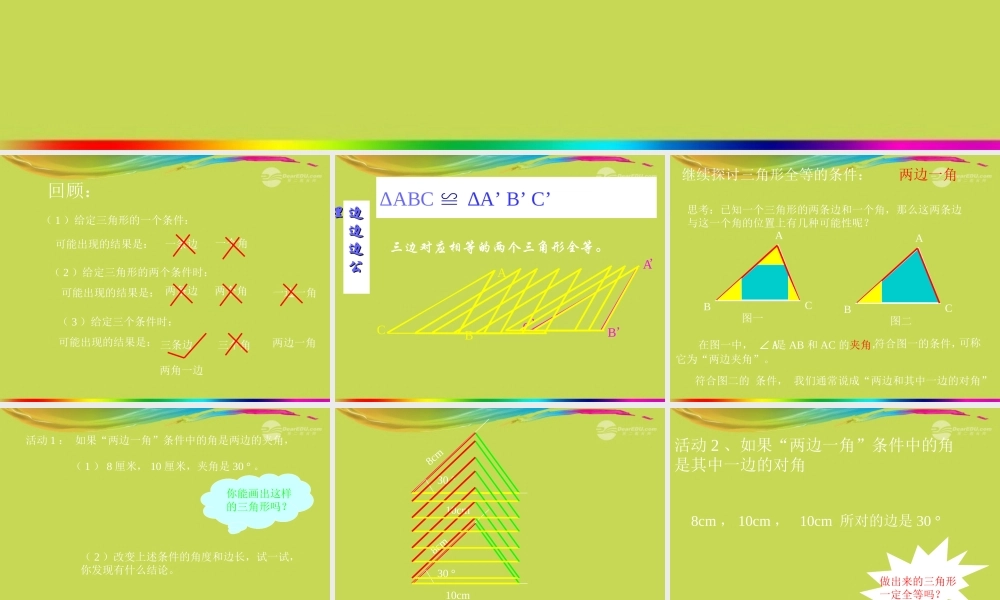
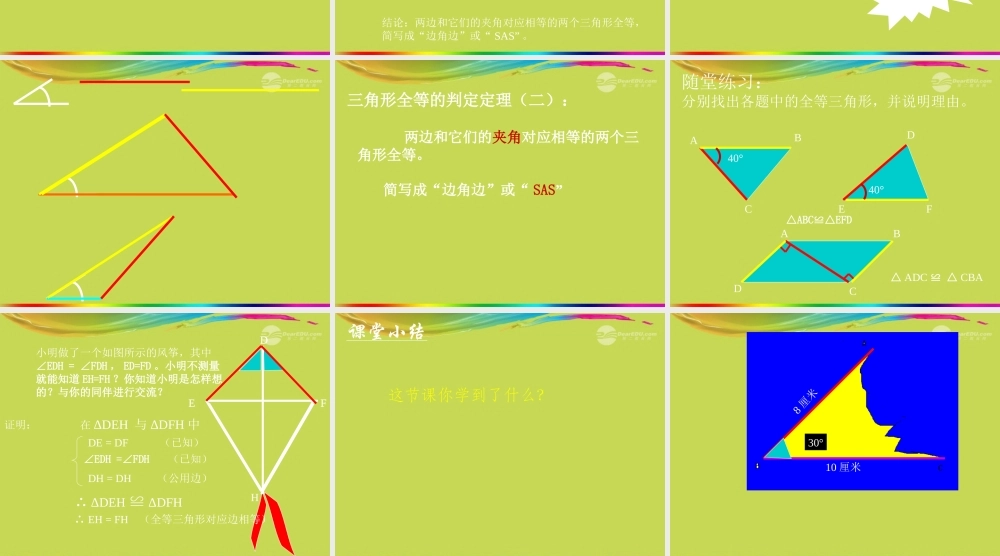
13.5全等三角形的判定回顾:(1)给定三角形的一个条件:可能出现的结果是:一条边一个角(2)给定三角形的两个条件时:可能出现的结果是:两条边两个角一边一角(3)给定三个条件时:可能出现的结果是:三个角三条边两边一角两角一边边边边公边边边公理理ABCABC‚‚‚ΔABC≌∆A’B’C’三边对应相等的两个三角形全等。继续探讨三角形全等的条件:两边一角思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?ABCABC图一图二在图一中,∠A是AB和AC的夹角,符合图一的条件,可称符合图二的条件,我们通常说成“两边和其中一边的对角”它为“两边夹角”。活动1:如果“两边一角”条件中的角是两边的夹角,(1)8厘米,10厘米,夹角是30°。你能画出这样的三角形吗?(2)改变上述条件的角度和边长,试一试,你发现有什么结论。结论:两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。30°8cm10cm10cm8cm30°活动2、如果“两边一角”条件中的角是其中一边的对角8cm,10cm,10cm所对的边是30°ni做出来的三角形一定全等吗?三角形全等的判定定理(二):两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”ACBDEFABCD△ABC≌△EFD△ADC≌△CBA40°40°随堂练习:分别找出各题中的全等三角形,并说明理由。小明做了一个如图所示的风筝,其中∠EDH=∠FDH,ED=FD。小明不测量就能知道EH=FH?你知道小明是怎样想的?与你的同伴进行交流?HDEFDEF证明:在ΔDEH与ΔDFH中DE=DF(已知)∠EDH=∠FDH(已知)DH=DH(公用边)∴ΔDEH≌ΔDFH∴EH=FH(全等三角形对应边相等)课堂小结这节课你学到了什么?8厘米10厘米30°