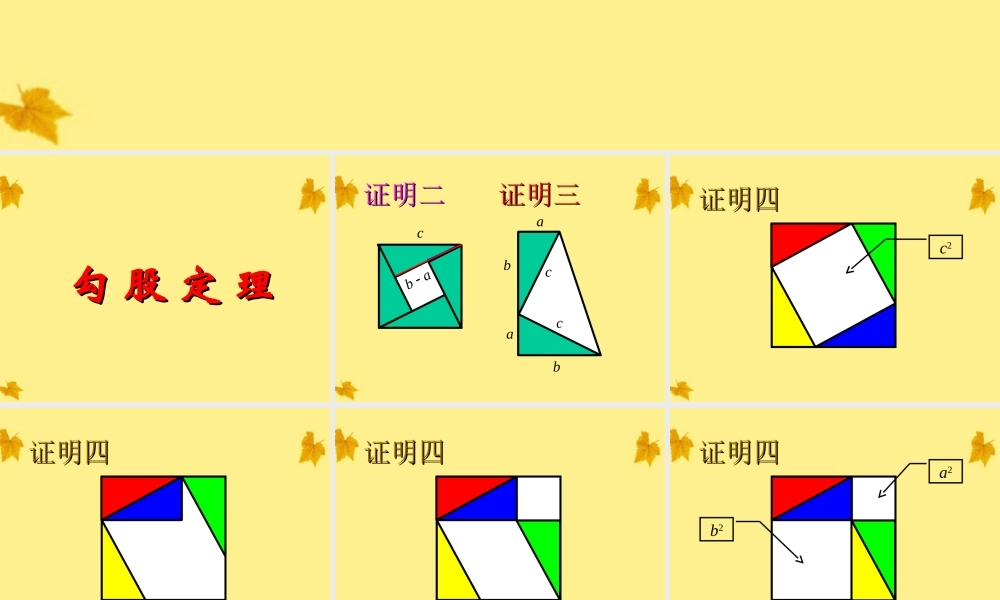
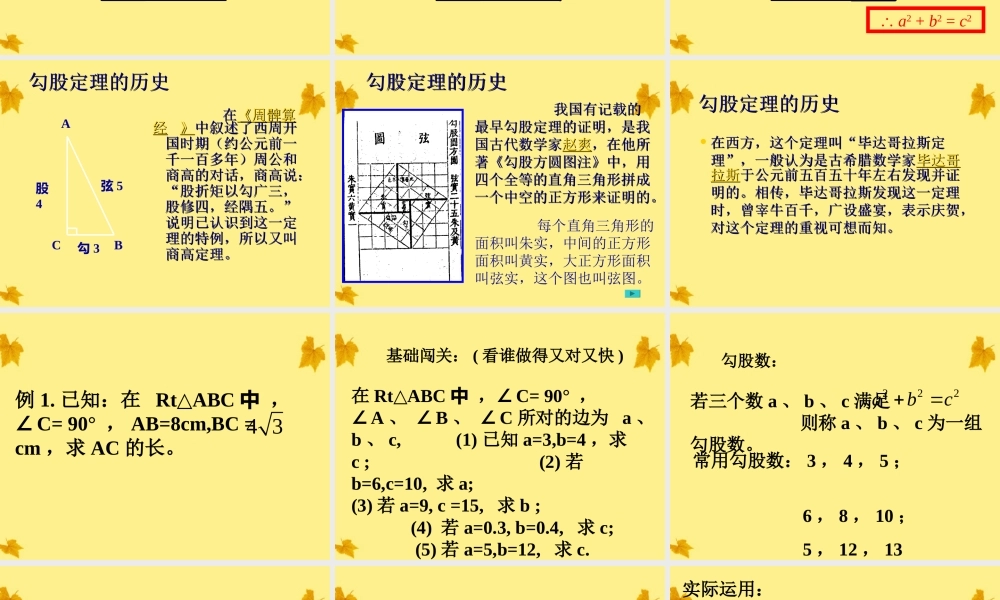
勾股定勾股定理理证明二证明二cbaaabbcc证明证明三三证明四证明四c2证明四证明四证明四证明四证明四证明四a2b2a2+b2=c2勾股定理的历史勾股定理的历史在在《《周髀算周髀算经经》》中叙述了西周开中叙述了西周开国时期(约公元前一国时期(约公元前一千一百多年)周公和千一百多年)周公和商高的对话,商高说:商高的对话,商高说:“股折矩以勾广三,“股折矩以勾广三,股修四,经隅五。”股修四,经隅五。”说明已认识到这一定说明已认识到这一定理的特例,所以又叫理的特例,所以又叫商高定理。商高定理。BCA勾3弦5股4勾股定理的历史勾股定理的历史我国有记载的我国有记载的最早勾股定理的证明,是我最早勾股定理的证明,是我国古代数学家国古代数学家赵爽赵爽,在他所,在他所著著《《勾股方圆图注勾股方圆图注》》中,用中,用四个全等的直角三角形拼成四个全等的直角三角形拼成一个中空的正方形来证明的。一个中空的正方形来证明的。每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。勾股定理的历史勾股定理的历史•在西方,这个定理叫“毕达哥拉斯定在西方,这个定理叫“毕达哥拉斯定理”,一般认为是古希腊数学家理”,一般认为是古希腊数学家毕达哥毕达哥拉斯拉斯于公元前五百五十年左右发现并证于公元前五百五十年左右发现并证明的。相传,毕达哥拉斯发现这一定理明的。相传,毕达哥拉斯发现这一定理时,曾宰牛百千,广设盛宴,表示庆贺,时,曾宰牛百千,广设盛宴,表示庆贺,对这个定理的重视可想而知。对这个定理的重视可想而知。例1.已知:在RtABC△中,∠C=90°,AB=8cm,BC=cm,求AC的长。43基础闯关:(看谁做得又对又快)在RtABC△中,∠C=90°,∠A、∠B、∠C所对的边为a、b、c,(1)已知a=3,b=4,求c;(2)若b=6,c=10,求a;(3)若a=9,c=15,求b;(4)若a=0.3,b=0.4,求c;(5)若a=5,b=12,求c.勾股数:若三个数a、b、c满足则称a、b、c为一组勾股数。222abc常用勾股数:3,4,5;6,8,10;5,12,13探索规律:3,4,5;6,8,10;9,12,15;0.3,0.4,0.5观察下面几组勾股数,你能发现什么规律?牛刀小试:例2.已知:在RtABC△中,∠C=90°,∠A=30°,BC=1,求AB、AC的长。例3.一棵高18米的大树被风刮断,树顶落在离树根12米处,研究人员要查看断痕,需要从树底开始爬多高?实际运用:开启智慧:已知:等腰△ABC中,AB=AC=3,BC=4,求△ABC的面积。本节课你有哪些收获?