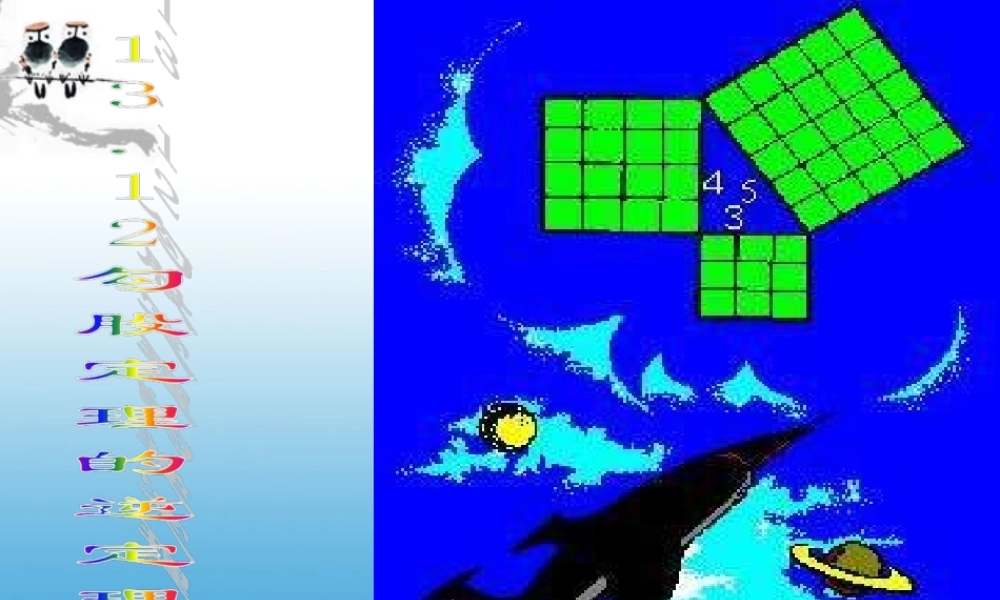
勾股定理:直角三角形两条直角边的平方和等于斜边的平方。acbBCAacbBCA如图:a2+b2=c2或BC2+AC2=AB2(1)a=5,b=12,则c=___(2)b=7,c=9,则a=_____.若一个直角三角形的两条边长分别是3㎝和4㎝,求这个直角三角形的周长?•古埃及人曾用下面的方法得到直角:他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,就会得到一个直角三角形。其直角在第4个结处。•他们真的能够得到直角三角形吗?(1)画三个三角形,使其边长分别为3㎝,4㎝,5㎝;5㎝,12㎝,13㎝;8㎝,15㎝,17㎝(2)算一算较短两条边长的平方和与最长一条边长的平方是否相等?(3)用量角器量一量,它们都是什么三角形?由此,你能得到怎样的猜想?如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。(1)上述结论中,哪条边所对的角是直角?(2)如果三角形中较短两边的平方和不等于最长的平方,那么这个三角形是直角三角形吗?例1.根据下列条件,分别判断以a,b,c为边的三角形是不是直角三角形?(1)a=7,b=24,c=25;(2)a=,b=1,c=.3232练一练:根据下列条件,判断下面以a,b,c为边的三角形是不是直角三角形?(1)a=20,b=21,c=29(2)a=5,b=7,c=8(3)a=,b=,c=2(4)a:b:c=2:3:473能够成为直角三角形三边长的三个正整数,称为勾股数(或勾股弦数)。例2如果△ABC的三边长分别为a,b,c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)则△ABC是直角三角形解:∵a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数)∴a2+b2=(m2-n2)2+(2mn)2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4=(m2+n2)2=c2∴△ABC是直角三角形。CcbaAB(1)、如图,图形A,B,C都是正方形且A的面积+B的面积=C的面积,则图中的三角形是什么三角形?练一练:(2)、完成书P43课内练习T2如图:边长为4的正方形ABCD中,F是DC的中点,且CE=BC,则AFEF⊥,试说明理由41ABDCFE解:连接AE∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC∴根据勾股定理,在RtADF△,AF2=AD2+DF2=20RtEFC△,EF2=EC2+FC2=5RtABE△,AE2=AB2+BE2=25∴AD=4,DF=2,FC=2,EC=1∴AE2=EF2+AF2AEF=90°∴∠即AFEF⊥本节课你学到了什么?还有什么困惑?课本作业题节选作业本