北京课改初中数学九上《20.2二次函数y=ax^2+bx+c(a≠0) 的图象》PPT课件 (7).pptVIP免费

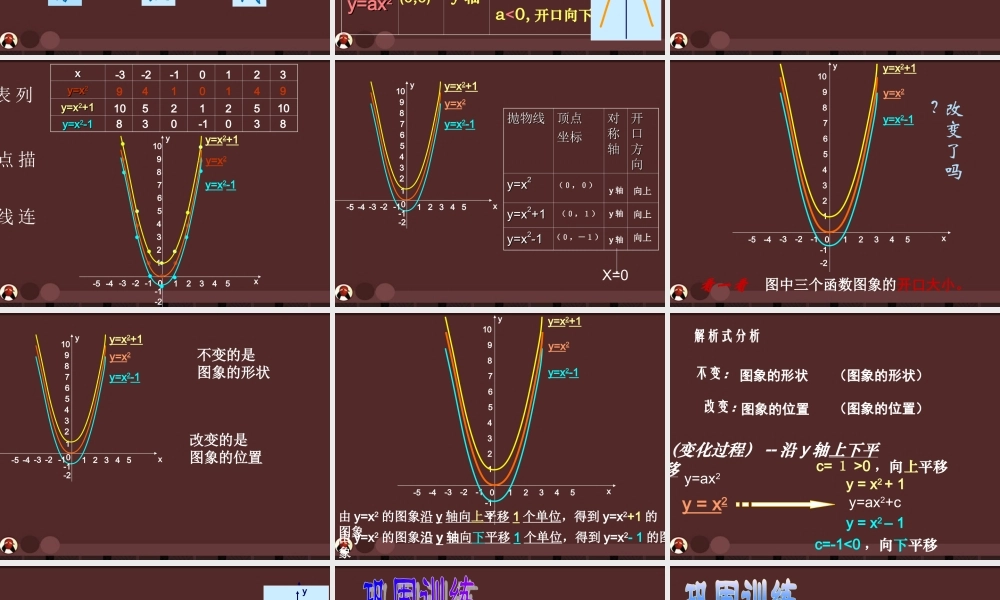
二次函数的图象y=ax2+bx+c(a≠0)知识与技能：1．学生掌握y=ax2+c与y=ax2的图象在平面直角坐标系中的位置特点及移动方法；2．学生掌握y=ax2+c的图象的开口方向、对称轴、顶点坐标；过程与方法：通过比较抛物线的相互关系，培养学生观察、分析、归纳、总结的能力；渗透数形结合的数学思想方法；情感态度价值观：通过本节课的教学，向学生进行事物间是相互联系及相互转化的。教学重点：1．y=ax2+c与y=ax2的图象在平面直角坐标系中的位置特点及移动方法；2．y=ax2+c的图象的开口方向、对称轴、顶点坐标。教学难点:y=ax2+c与y=ax2的图象在平面直角坐标系中的位置特点及移动方法；教学方法：探究法教学用具：多媒体2axy画图象的方法：列表描点连线2axy的图象特征：抛物抛物线线顶点顶点坐标坐标对称对称轴轴开口方向开口方向y=axy=ax22(0,0)y轴a>0,开口向上a<0,开口向下xy0在同一坐标系中，作出下列函数的图象，并观察c取不同的值时，二次函数y=ax2+c的图象和y=ax2的图象有怎样的关系:(1)y=x2(2)y=x2+1(3)y=x2-1xxy=xy=x22y=xy=x22+1+1y=xy=x22-1-1xy012345135-1-3-224678910-1-2-4-5-3-2-101231052191052410149830038-1y=x2+1y=x2-1y=x2列表描点连线xy012345135-1-3-224678910-1-2-4-5y=x2+1y=x2y=x2-1抛物线抛物线顶点顶点坐标坐标对对称称轴轴开开口口方方向向y=xy=x22y=xy=x22+1+1y=xy=x22-1-1（０，０）（０，１）（０，－１）y轴y轴y轴向上向上向上X=0xy012345135-1-3-224678910-1-2-4-5y=x2+1y=x2y=x2-1看一看图中三个函数图象的开口大小。改变了吗？xy012345135-1-3-224678910-1-2-4-5y=x2+1y=x2y=x2-1不变的是图象的形状改变的是图象的位置xy012345135-1-3-224678910-1-2-4-5y=x2+1y=x2y=x2-1由y=x2的图象沿y轴向上平移1个单位，得到y=x2+1的图象由y=x2的图象沿y轴向下平移1个单位，得到y=x2-1的图象不变：图象的位置图象的形状改变：解析式分析（变化过程）--沿y轴上下平移y=x2+1y=x2–1y=x2（图象的形状）（图象的位置）c=１>0，向上平移c=-1<0，向下平移y=ax2y=ax2+ccaxy2xy0抛物线抛物线顶顶点点坐坐标标对对称称轴轴开口方向开口方向y=axy=ax22+c+c(0,c)y轴a>0,开口向上a<0,开口向下的图象特征二次函数(1)把抛物线沿y轴向平移__个单位，得到的抛物线解析式为。上422xy422xy试一试新抛物线的顶点坐标是______，对称轴是____，开口方向______。（0,４）y轴向下(2)把抛物线的图象沿y轴向下平移7个单位，得到的抛物线解析式...