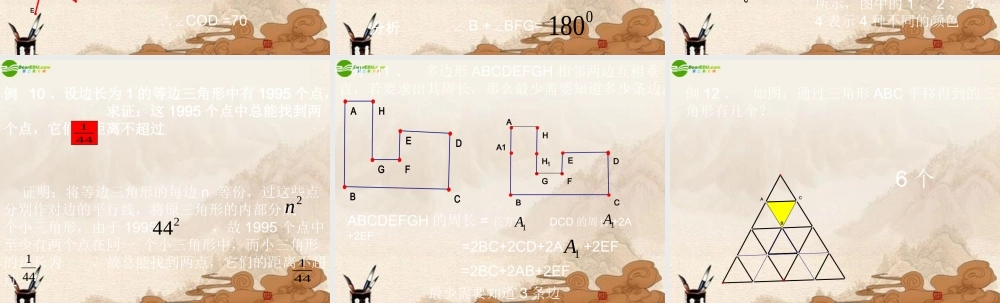
4.14相交线与平行线专题讲析同一平面内的两条不重合直线的位置是相交或平行。相交关系最重要的是垂直。平行线中的平行公理及推论、平行线的性质、判定等的应用是重点。1、平面上互不重合的三条直线的交点数是个如果两两相交的直线共有多少个交点?2、我们知道,两条直线相交,有且只有一个交点,三条直线相交,最多有三个交点。四条直线相交,最多有多少个交点?五条呢?N条呢?3、一条直线分平面为两个部分,二条直线分平面最多为四个部分。那么五条直线分平面最多为多少个部分?一般地,N条直线分平面最多为多少个部分?4、你条直线相交于一点,问共有多少对对顶角?5、已知O是直线AC上的点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOC=EOC∠,∠DOE=求∠EOC的度数?21070ABEDC设∠DOB=BOE=∠0x0x{X+y=702x+3y=180例6、∠AOB为直角,∠AOC为锐角,ON平分∠AOC,OM平分∠COB,求∠MON的度数ABCONM∠MON=MOC∠-∠NOC2121=BOC∠-∠AOC2121=(∠AOB+AOC∠)-∠AOC21=AOB∠例7、由点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=,OF平分∠BOC,OE平分∠AOD,若∠EOF=,求∠COD的度数。0900170BACDOFEX+y+90=190∴X+y=100又∵x+y+COD=170∠∴∠COD=70设∠COF=DOE=∠则有0x0y例8、已知ADBC⊥,EFBC⊥,∠1=2∠,求证ABGF∥12BCAFDEG∠B+BFG=∠0180分析例9、将图中的8条线段AB、BC、CD、AD、AE、BE、CE、DE着色,使具有公共端点的线段的颜色不相同,则最少需要多少种颜色?EBACD32411432由于以E为线段有4条,故最少要4种颜色,如图所示,图中的1、2、3、4表示4种不同的颜色例10、设边长为1的等边三角形中有1995个点,求证:这1995个点中总能找到两个点,它们的距离不超过441证明:将等边三角形的每边n等份,过这些点分别作对边的平行线,将原三角形的内部分成个小三角形,由于1995>,故1995个点中至少有两个点在同一个小三角形中,而小三角形的边长为,故总能找到两点,它们的距离不超过2n244441441例11、多边形ABCDEFGH相邻两边互相垂直,若要求出其周长,那么最少需要知道多少条边。ABCHGFEDEFGHDCBAA1H1=2BC+2AB+2EF=2BC+2CD+2A+2EF1AABCDEFGH的周长=长方形DCD的周长+2A+2EF1A1A最少需要知道3条边例12、如图:通过三角形ABC平移得到的三角形有几个?BCA6个