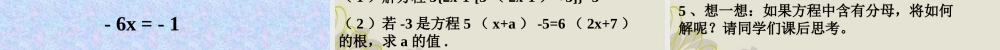一元一次方程根据等式的性质“如果a=b,那么b=a”填空:(1)如果-2=x,那么x=____.(2)如果1=a+b,那么a+b=____.(3)如果-2-x=0,移项得-2=x,那么x=____.(4)如果c=-d,在等式两边都乘以-1得-c=d,那么d=____.例一:解方程:5x+2=7x-8解法1:移项,得2+8=7x-5x合并同类项,得10=2x即2x=10.系数化为1,得x=5解法2:移项,得5x-7x=-8-2合并同类项,得-2x=-10系数化为1,得x=5例2:解方程2(x-2)-3(4x-1)=9(1-x)解:去括号,得2x-4-12x+3=9-9x移项,得2x-12x+9x=9+4-3合并同类项,得-x=10系数化为1,得x=-10下面方程式的解法对不对,如果不对,应怎样改正?解方程2(x+3)-5(1-x)=3(x-1)解:2x+3-5-5x=3x-32x-5x-3x=-3+5-3-6x=-1∴1/6练习A级:(1)2x+5=25-8x(2)5(x+2)=2(2x+7)B级:(1)-7=5+x(2)3(2y+1)=2(1+y)+3(y+3)C级:(1)解方程3{2x-1-[3(2x-1)+3]}=5(2)若-3是方程5(x+a)-5=6(2x+7)的根,求a的值.1、本节课我们主要学习了什么?2、学习解方程运用的法则是什么?3、运用法则时要注意什么?4、解方程的一般步骤有哪些?5、想一想:如果方程中含有分母,将如何解呢?请同学们课后思考。小结