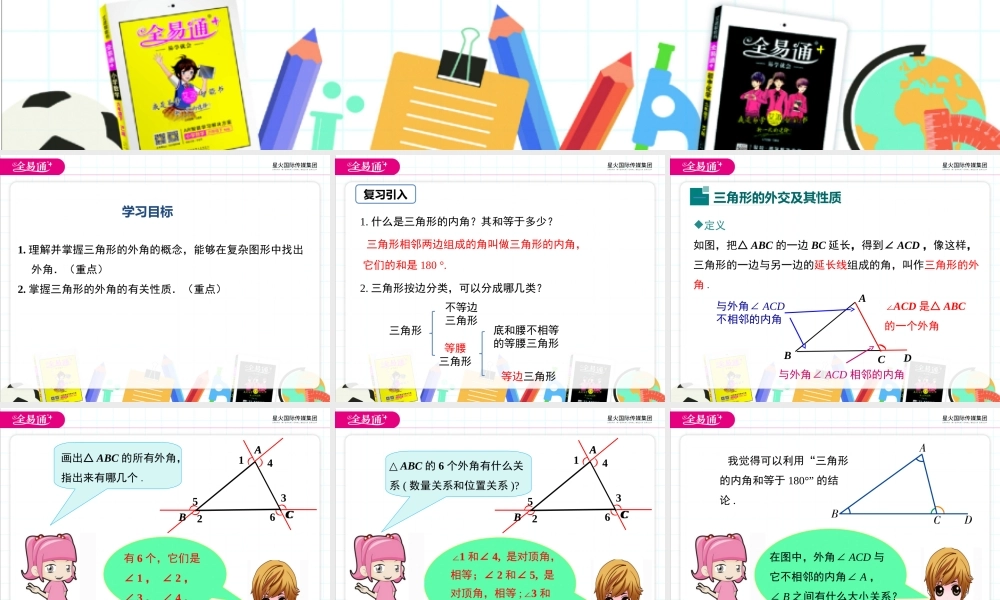
第九章三角形9.2三角形的内角和外角第2课时1.理解并掌握三角形的外角的概念,能够在复杂图形中找出外角.(重点)2.掌握三角形的外角的有关性质.(重点)学习目标复习引入1.什么是三角形的内角?其和等于多少?三角形相邻两边组成的角叫做三角形的内角,它们的和是180°.2.三角形按边分类,可以分成哪几类?三角形不等边三角形等腰三角形底和腰不相等的等腰三角形等边三角形三角形的外交及其性质一定义如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫作三角形的外角.ABCD(∠ACD是△ABC的一个外角与外角∠ACD不相邻的内角与外角∠ACD相邻的内角画出△ABC的所有外角,指出来有哪几个.((((((ABC123456ABC有6个,它们是∠1,∠2,∠3,∠4,∠5,∠6.△ABC的6个外角有什么关系(数量关系和位置关系)?((((((ABC123456ABC∠1和∠4,是对顶角,相等;∠2和∠5,是对顶角,相等;3∠和∠6,是对顶角,相等.在图中,外角∠ACD与它不相邻的内角∠A,∠B之间有什么大小关系?我觉得可以利用“三角形的内角和等于180°”的结论. ∠ACD+∠ACB=180°,(补角的定义)∠A+∠B+∠ACB=180°,(三角形的内角和定理)∴∠ACD-∠A-∠B=0.∴∠ACD=∠A+∠B. ∠A>0,∠B>0,∴∠ACD>∠A,∠ACD>∠B.知识要点三角形的外角的性质三角形的一个外角等于与它不相邻的两个内角的和.三角形的一个外角大于与它不相邻的任意一个内角.典例精析例1如图,∠BCD=92°,∠A=27°,∠BED=44°,求(1)∠B的度数;ACDEB解:(1)在△ABC中, ∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),∠BCD=92°,∠A=27°,(已知)∴∠B=∠BCD-∠A=92°-27°=65°;(2)在△BEF中, ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),∠BED=44°(已知),∠B=65°,(已知)∴∠BFD=44°+65°=109°.ACDEB(2)∠BFD的度数;例2(一题多解)如图,计算∠BDC.ABCD(((51°20°30°思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.ABCD(((51°20°30°解:(解法一)连接AD并延长于点E.在△ABD中,∠1+∠ABD=3∠,在△ACD中,∠2+∠ACD=4.∠因为∠BDC=3+4∠∠,∠BAC=1+2∠∠,所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.E))12)3)4ABCD(((51°20°30°E)1(解法二)延长BD交AC于点E.在△ABE中,∠1=∠ABE+∠BAE,在△ECD中,∠BDC=1+∠∠ECD.所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.(解法三...