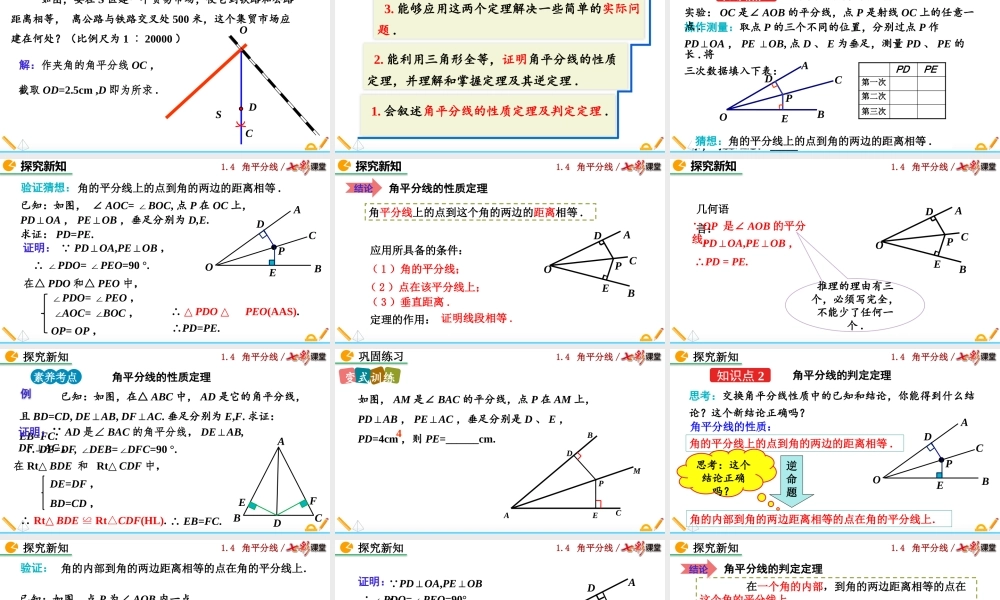
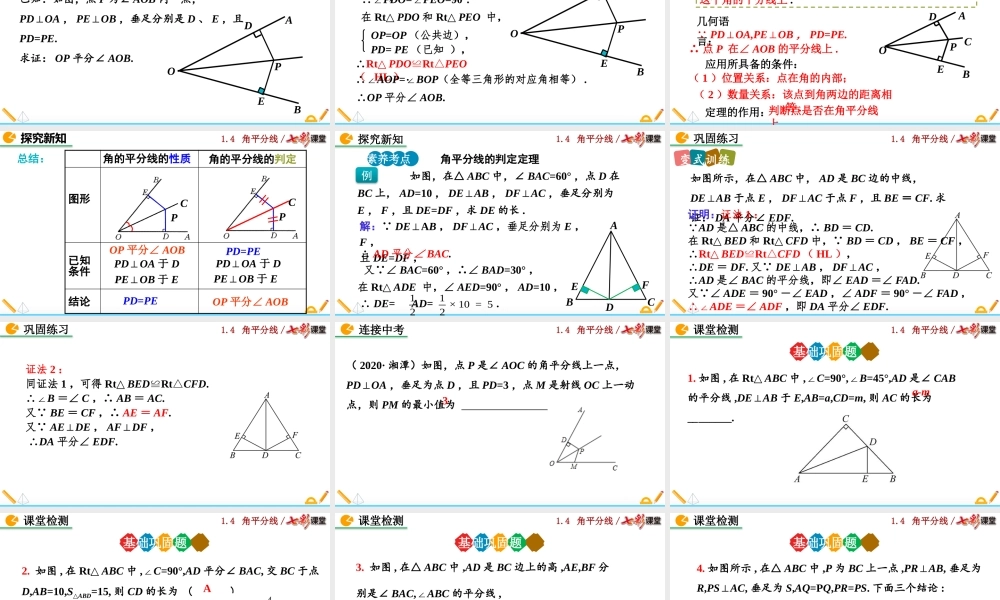
1.4角平分线/1.4角平分线(第1课时)北师大版八年级数学下册1.4角平分线/如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,离公路与铁路交叉处500米,这个集贸市场应建在何处?(比例尺为1︰20000)DCS解:作夹角的角平分线OC,截取OD=2.5cm,D即为所求.O导入新知1.4角平分线/1.会叙述角平分线的性质定理及判定定理.2.能利用三角形全等,证明角平分线的性质定理,并理解和掌握定理及其逆定理.素养目标3.能够应用这两个定理解决一些简单的实际问题.1.4角平分线/探究新知知识点1角平分线的性质定理操作测量:取点P的三个不同的位置,分别过点P作PD⊥OA,PE⊥OB,点D、E为垂足,测量PD、PE的长.将三次数据填入下表:观察测量结果,猜想线段PD与PE的大小关系,写出结论:_____PDPE第一次第二次第三次COBAPD=PEPDE实验:OC是∠AOB的平分线,点P是射线OC上的任意一点.猜想:角的平分线上的点到角的两边的距离相等.1.4角平分线/已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.求证:PD=PE.验证猜想:角的平分线上的点到角的两边的距离相等.PAOBCDE证明: PD⊥OA,PE⊥OB,∴∠PDO=∠PEO=90°.在△PDO和△PEO中,∠PDO=∠PEO,∠AOC=BOC∠,OP=OP,∴△PDO△△PEO(AAS).∴PD=PE.探究新知1.4角平分线/角平分线上的点到这个角的两边的距离相等.角平分线的性质定理结论应用所具备的条件:(1)角的平分线;(2)点在该平分线上;(3)垂直距离.BADOPEC定理的作用:证明线段相等.探究新知1.4角平分线/几何语言: OP是∠AOB的平分线,∴PD=PE.推理的理由有三个,必须写完全,不能少了任何一个.PD⊥OA,PE⊥OB,探究新知BADOPEC1.4角平分线/角平分线的性质定理素养考点1探究新知已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC.垂足分别为E,F.求证:EB=FC.例ABCDEF证明: AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF,DEB=DFC∠∠=90°.在Rt△BDE和Rt△CDF中,DE=DF,BD=CD,∴Rt△BDERt≌△CDF(HL).∴EB=FC.1.4角平分线/巩固练习变式训练如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,PD=4cm,则PE=______cm.BACPMDE41.4角平分线/知识点2角平分线的判定定理PAOBCDE角的内部到角的两边距离相等的点在角的平分线上.思考:交换角平分线性质中的已知和结论,你能得到什么结论?这个新结论正确吗?角平分线的性质:角的平分线上的点到角的两边的距离相等.思考:这个结论正确吗?逆命题探究新...