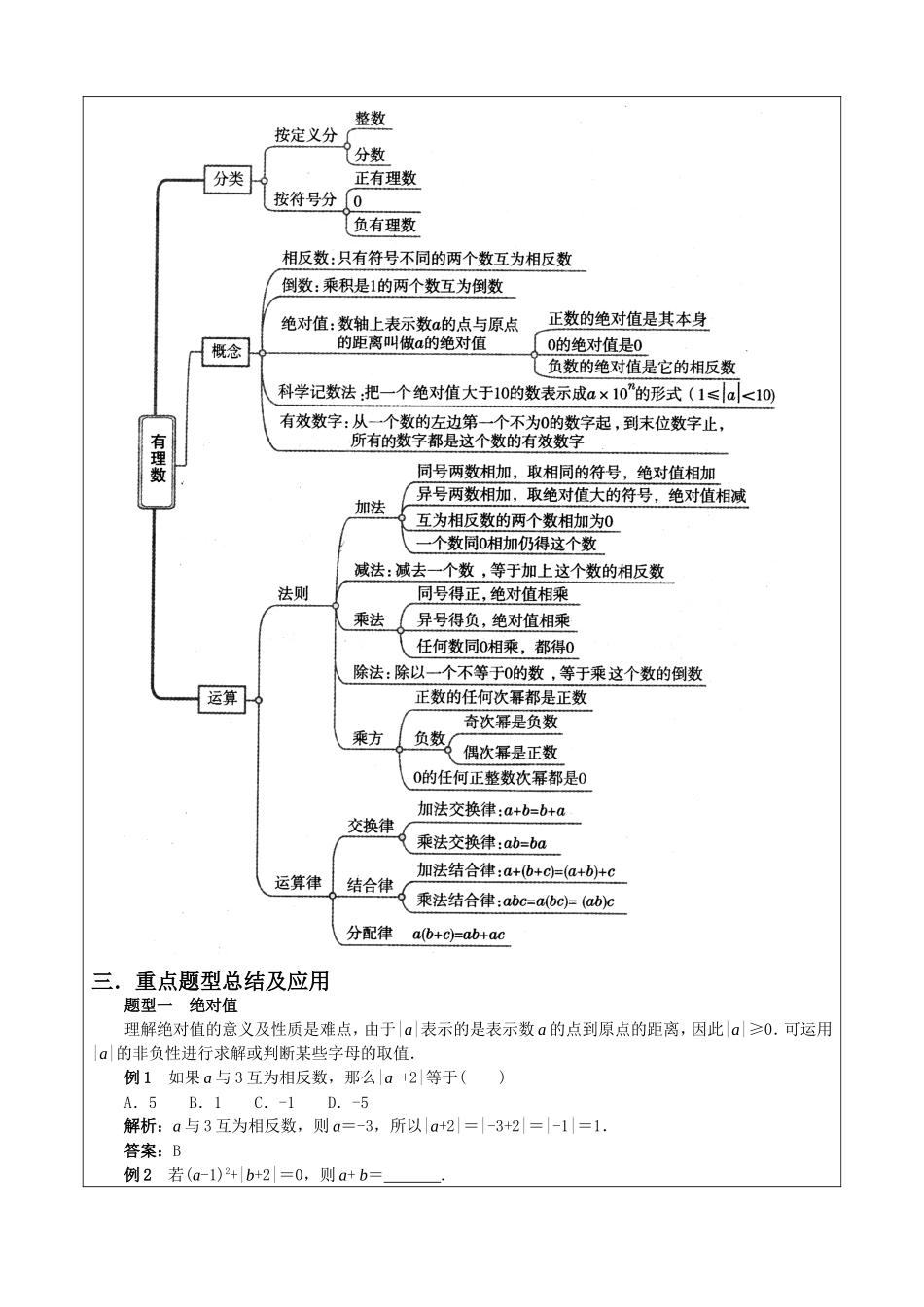
6(下)数学第五章有理数复习课教案教师姓名:管习光年级:六年级学员姓名:李悦祺课次:总课次8,第1次授课时间课题有理数教学目标及重难点教学目标:能够运用有理数的运算法则正确进行运算,并且能够掌握好有理数的运算顺序及符号的确定。教学重点:有理数的意义及运算。教学难点:负数概念的建立以及对有理数运算法则的理解。课前检查作业完成情况:优□良□中□差□建议:教学步骤一.知识梳理1、数轴规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。在数轴上表示的两个数,右边的数总比左边的数大。2、相反数实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a与b互为相反数,则有a+b=0,a=—b,反之亦成立。3、绝对值一个数的绝对值就是表示这个数的点与原点的距离,|a|≥0。零的绝对值时它本身,也可看成它的相反数,若|a|=a,则a≥0;若|a|=-a,则a≤0。正数大于零,负数小于零,正数大于一切负数,两个负数,绝对值大的反而小。4、倒数如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。5、科学记数法把一个数写做的形式,其中,n是整数,这种记数法叫做科学记数法。二.知识网络结构图三.重点题型总结及应用题型一绝对值理解绝对值的意义及性质是难点,由于|a|表示的是表示数a的点到原点的距离,因此|a|≥0.可运用|a|的非负性进行求解或判断某些字母的取值.例1如果a与3互为相反数,那么|a+2|等于()A.5B.1C.-1D.-5解析:a与3互为相反数,则a=-3,所以|a+2|=|-3+2|=|-1|=1.答案:B例2若(a-1)2+|b+2|=0,则a+b=.解析:由于(a-1)2≥0,|b+2|≥0,又(a-1)2与|b+2|互为相反数,因此(a-1)2=0且|b+2|=0,则a=1,b=-2,所以a+b=-1.答案:-1规律若几个非负数的和为0,则这几个数分别为0.题型二有理数的运算有理数的运算包括加减法、乘除法及乘方,是初中数学运算的基础.要熟记法则,灵活运算,进行混合运算时,还要注意运算顺序及运算律的应用.例3(-1)2011的相反数是()A.1B.-1C.2011D.-2011解析:由于指数2011为奇数,所以(-1)2011=-1,其相反数为1.答案:A例4计算:(1);(2).解:(1)=4-9×=4-4=0.(2)===题型三运用运算律简化运算过程运用加法的交换律、结合律,把某些具有相同属性的数(如正数、负数、分数中的分母具有倍数关系、相反...