2002年数学三真题答案解析.pdfVIP免费

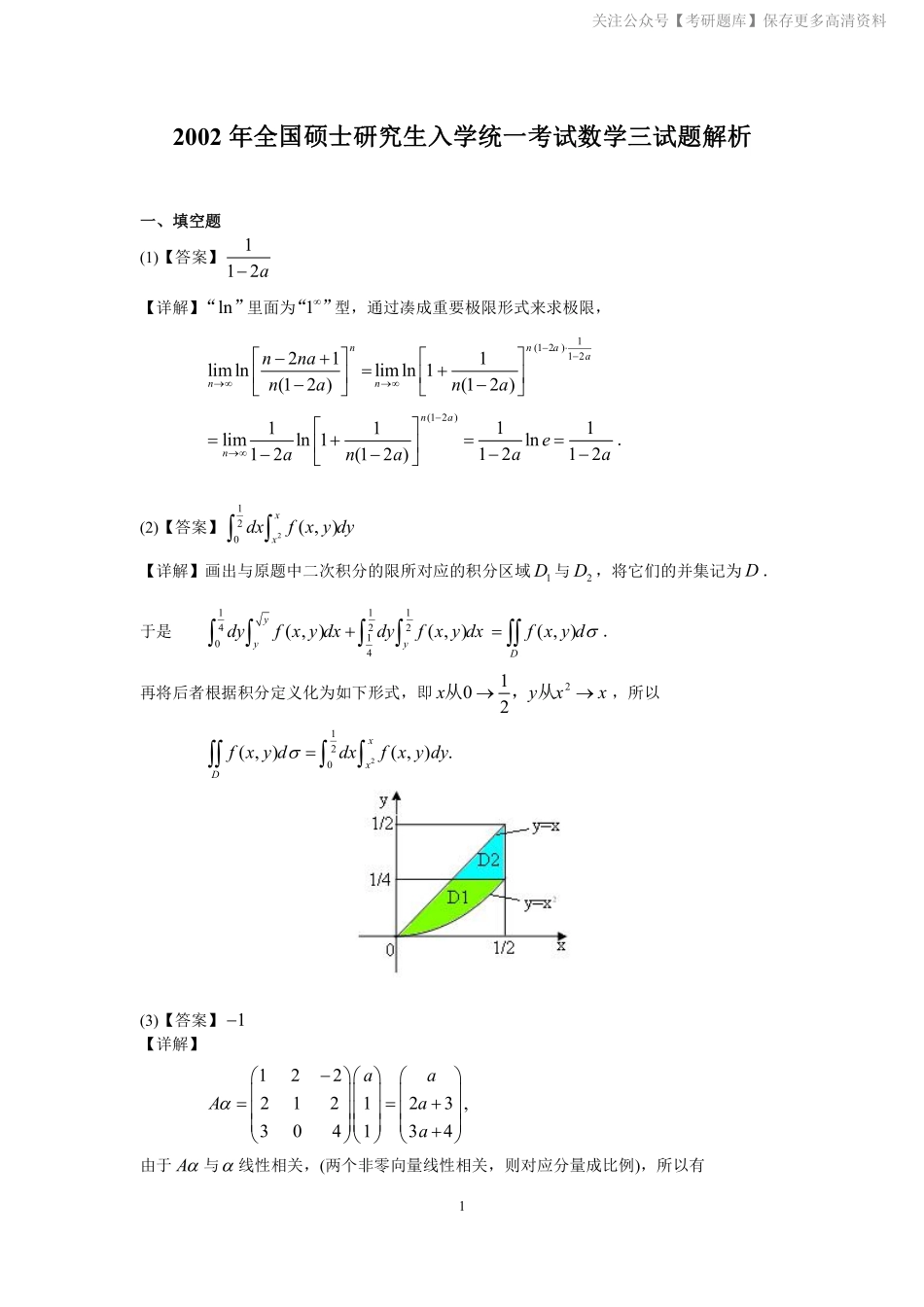
12002年全国硕士研究生入学统一考试数学三试题解析一、填空题(1)【答案】112a【详解】ln“”里面为1“”型，通过凑成重要极限形式来求极限，1(12)12211limlnlimln1(12)(12)nnaannnnanana(12)11limln112(12)nanana11ln1212eaa．(2)【答案】2120(,)xxdxfxydy【详解】画出与原题中二次积分的限所对应的积分区域1D与2D，将它们的并集记为D．于是111422104(,)(,)yyydyfxydxdyfxydx(,)Dfxyd．再将后者根据积分定义化为如下形式，即2102xyxx从，从，所以2120(,)(,).xxDfxyddxfxydy(3)【答案】1【详解】122212123,304134aaAaa由于A与线性相关，(两个非零向量线性相关，则对应分量成比例)，所以有关注公众号【考研题库】保存更多高清资料2233411aaaa，得2334,1.aaa或,(0)Akk(两个非零向量线性相关，则其中一个可以由另一个线性表出)即231341aaaka，得2334akaakak，得1.(1)ak(4)【答案】0.02．【详解】2X、2Y和2X2Y都是01分布，而01分布的期望值恰为取1时的概率p．由离散型随机变量X和Y的联合概率分布表可得2X的可能取值为0和1，且2Y的可能取值也为0和1，且X和Y的边缘分布为00.070.180.150.4PX；10.080.320.200.6PX；10.070.080.15PY；00.180.320.5PY；10.150.200.35PY；故有X010.40.6Y1010.150.50.35220,00,00.18,PXYPXY220,10,10,10.070.150.22,PXYPXYPXY221,01,00.32,PXYPXY221,11,11,10.080.200.28,PXYPXYPXY而边缘分布律：2000.4PXPX，2110.6PXPX，2000.5PYPY，21110.150.350.5PYPYPY所以，22(,)XY的联合分布及其边缘分布为关注公众号【考研题库】保存更多高清资料32Y2X0100．180．220．4010．320．280．600．500．501由上表同理可求得22XY的分布律为22XY01P0．720．28所以由01分布的期望值恰为取1时的概率p得到：2222222222()0.5()0.60,(0.28...