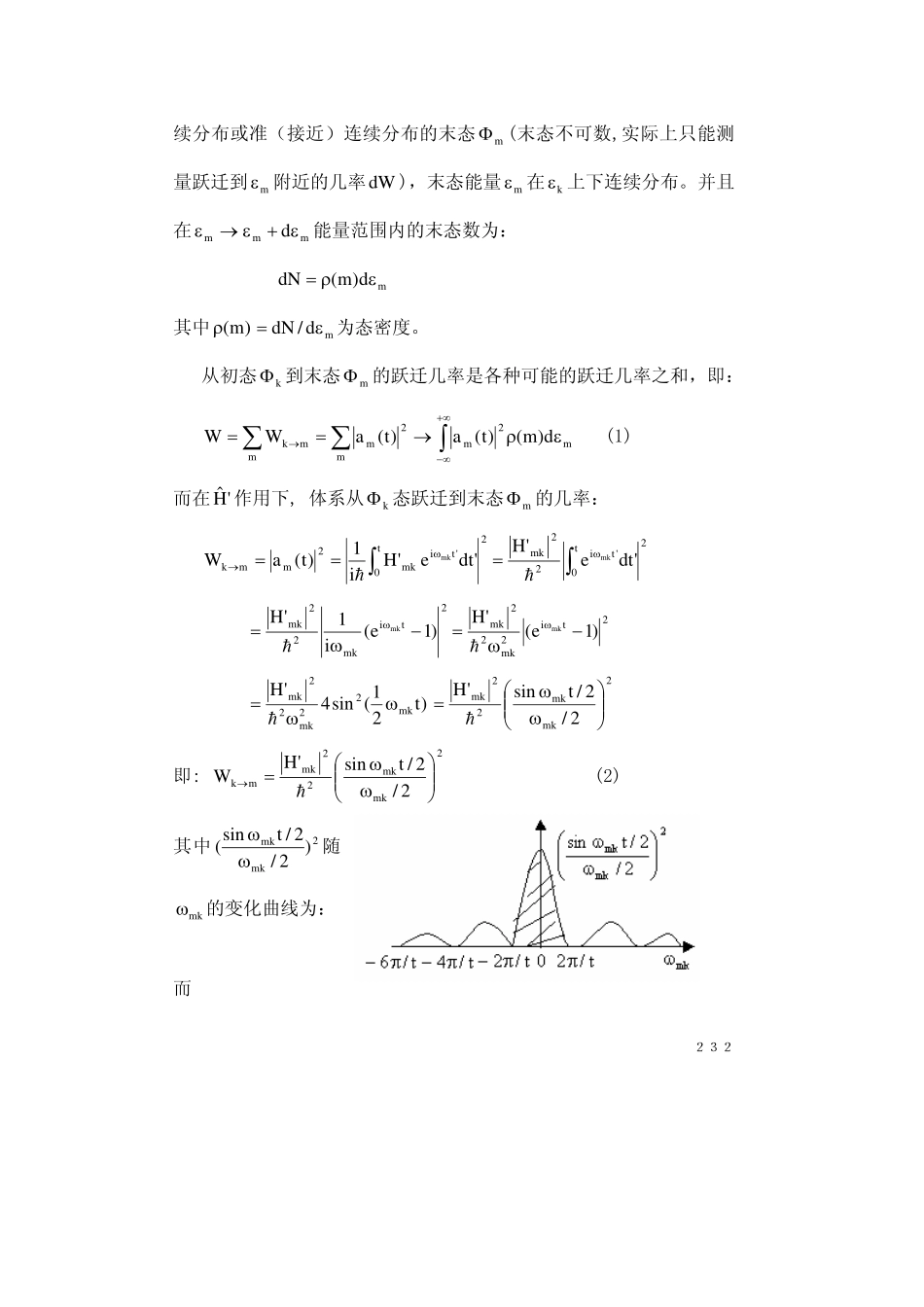
231§5.7跃迁几率重点:在常微扰和周期微扰下的跃迁几率难点:能量时间的测不准关系根据问题具体讨论跃迁几率的计算。一、常微扰1.实例例如:能量为kε的自由粒子被方波散射。设方波微扰表示为:⎩⎨⎧><≤≤=)t't,0't(,0)t't0(,V)t('Hˆ0该体系的特点是:①散射态能量本征值为连续谱,kε上下均允许取值;②方波可表示为各种单色波的迭加,即:∫+∞∞−ωωω=de)(c)t('Hˆti∫∫+∞∞−ω−ω−==ωt0'ti0'ti'dteV'dte)t('Hˆ)(c③能量为kε的粒子若吸收能量为ωh的光子,散射态能量为ω+εhk;若发射能量为ωh的光子,则末态能量为ω−εhk。∫+∞∞−ωωω=de)(c)t('Hˆti关于ω是连续的,粒子的本征值也是连续的,因而散射态的能量也是连续的.2.跃迁几率(∑→mk)⎩⎨⎧><≤≤=)t't,0't(,0)t't0(,ttancons'Hˆ设0't=时体系所处状态为kΦ,在'H作用下,体系从kΦ态跃迁到连232续分布或准(接近)连续分布的末态mΦ(末态不可数,实际上只能测量跃迁到mε附近的几率dW),末态能量mε在kε上下连续分布。并且在mmmdε+ε→ε能量范围内的末态数为:md)m(dNερ=其中)m(ρmd/dNε=为态密度。从初态kΦ到末态mΦ的跃迁几率是各种可能的跃迁几率之和,即:∑∑∫+∞∞−→ερ→==mmm2m2mmkd)m()t(a)t(aWW(1)而在'Hˆ作用下,体系从kΦ态跃迁到末态mΦ的几率:2t0'timk2mmk'dte'Hi1)t(aWmk∫ω→==h2t0'ti22mk'dte'Hmk∫ω=h2timk22mk)1e(i1'Hmk−ω=ωh2ti2mk22mk)1e('Hmk−ω=ωh)t21(sin4'Hmk22mk22mkωω=h2mkmk22mk2/2/tsin'H⎟⎟⎠⎞⎜⎜⎝⎛ωω=h即:2mkmk22mkmk2/2/tsin'HW⎟⎟⎠⎞⎜⎜⎝⎛ωω=→h(2)其中2mkmk)2/2/tsin(ωω随mkω的变化曲线为:而2332mkmk22mkmk2/2/tsin'HW⎟⎟⎠⎞⎜⎜⎝⎛ωω=→h2mkmk)2/2/tsin(ωω∝2mkmk2)2/t2/tsin(tωω=则在0mk=ω时,mkW→取得最大值。如果mε为分立谱,则可设一固定态mε,t时刻由kε跃迁到固定态mε的几率2mktW∝→,而跃迁速率tdt/dWmkmk∝=ω→→,与跃迁过程的统计解释矛盾,也与实验结果不符。如果末态为连续谱,t4t22t)egrate(intW2π=π⋅⋅∝,则跃迁速率π∝=ω4dt/)egrate(intdW与时间无关,与实验相符。下面考虑2mkmk)2/2/tsin(ωω的性质:下面我们看一个数学公式:)x(txxtsinlim22tδ=π∞→(3)即⎩⎨⎧≠=∞=π∞→0x,00x,)xtxtsin(tlim2t(满足)x(δ函数的定义式)性质:令uxt=,则:∫∫∞+∞−∞+∞−=ππ=π=π11duuusin1dxtxxtsin2222所以当t足够大时(微观足够大,宏观足...